
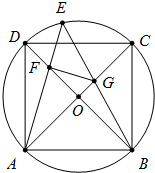
 如图,ABCD是圆O的内接正方形,E是劣弧CD上一点,EA交BD于F,EB交AC于G,且GF⊥AE.
如图,ABCD是圆O的内接正方形,E是劣弧CD上一点,EA交BD于F,EB交AC于G,且GF⊥AE.分析 (1)连接CE,由题意可知∠AOF=90°,由AC为圆的直径,∠AEC=90°,因此△AOF∽△AEC,根据三角形相似的性质,$\frac{AF}{AO}$=$\frac{AC}{AE}$,可知:AF•AE=AO•AC;
(2)设∠GOF=θ,⊙O的半径为1,则EC=2,分别求得AF和FG,在Rt△PMN中,∠AEB=∠FEG=∠ADB=45°,EF=FG,AF+FE=AE,整理得:1+tanθ=2cos2θ,由cosθ=$\frac{AO}{AF}$,tanθ=$\frac{FG}{AF}$,即可证明$\frac{{2A{O^2}}}{{A{F^2}}}-\frac{FG}{AF}=1$.
解答 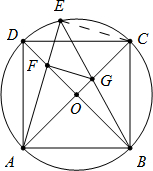 解:(1)证明:连接CE,
解:(1)证明:连接CE,
∵ABCD是圆O的内接正方形,AC和BD为三角形的对角线,
∴AC⊥BD,
∴∠AOF=90°,
由AC为圆的直径,
∴∠AEC=90°,
∴△AOF∽△AEC,
∴$\frac{AF}{AO}$=$\frac{AC}{AE}$,
∴AF•AE=AO•AC;
(2)证明:设∠GOF=θ,⊙O的半径为1,则EC=2,AE=AC•cosθ=2cosθ,
AF=$\frac{AO}{cosθ}$=$\frac{1}{cosθ}$,
FG=AF•tanθ=$\frac{tanθ}{cosθ}$,
在Rt△PMN中,∠AEB=∠FEG=∠ADB=45°,
∴EF=FG,
∵AF+FE=AE,
∴$\frac{1}{cosθ}$+$\frac{tanθ}{cosθ}$=2cosθ,
∴1+tanθ=2cos2θ,
∴2cos2θ-tanθ=1,
在RT△AOF中,cosθ=$\frac{AO}{AF}$,
在RT△AFG中,tanθ=$\frac{FG}{AF}$,
∴$\frac{{2A{O^2}}}{{A{F^2}}}-\frac{FG}{AF}=1$.
点评 本题考查圆方程的综合应用,考查正方形的性质,圆周角定理,相似三角形的性质,考查数形结合思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,1] | C. | (1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有95%的把握认为两者有关 | |
| B. | 约有95%的心脏病患者使用药物有作用 | |
| C. | 有99%的把握认为两者有关 | |
| D. | 约有99%的心脏病患者使用药物有作用 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,100] | B. | [36,64] | C. | (36,100) | D. | [6,10] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -256 | B. | 64 | C. | -64 | D. | 256 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com