
| A. | [0,100] | B. | [36,64] | C. | (36,100) | D. | [6,10] |
分析 根据已知条件判断出△ABC为Rt△,然后以点C为坐标原点,射线CA,CB分别为x,y轴正方向建立直角坐标系,设$\overrightarrow{CM}=\overrightarrow{CA}+λ\overrightarrow{AB}$,把$\overrightarrow{CM}$•$\overrightarrow{CA}$+$\overrightarrow{CM}$•$\overrightarrow{CB}$转化为含有λ的代数式,由λ的范围可得$\overrightarrow{CM}$•$\overrightarrow{CA}$+$\overrightarrow{CM}$•$\overrightarrow{CB}$=$\overrightarrow{CM}•(\overrightarrow{CA}+\overrightarrow{CB})$的取值范围.
解答 解:∵AC=6,BC=8,AB=10,∴AC2+BC2=AB2,即△ABC为直角三角形.
以点C为坐标原点,射线CA,CB分别为x,y轴正方向建立直角坐标系,
则A(6,0),B(0,8).
设$\overrightarrow{CM}=\overrightarrow{CA}+λ\overrightarrow{AB}$=(6,0)+λ(-6,8)=(6-6λ,8λ).
其中0≤λ≤1,$\overrightarrow{CM}$•$\overrightarrow{CA}$+$\overrightarrow{CM}$•$\overrightarrow{CB}$=$\overrightarrow{CM}•(\overrightarrow{CA}+\overrightarrow{CB})$=(6-6λ,8λ)•(6,8)=36+28λ.
∵0≤λ≤1,∴36≤$\overrightarrow{CM}$•$\overrightarrow{CA}$+$\overrightarrow{CM}$•$\overrightarrow{CB}$≤64.
故选:B.
点评 本题考查直角三角形边的关系,以及向量减法的几何意义,向量数量积的计算公式,三角函数的定义,以及数形结合解题的方法,是中档题.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
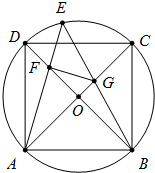 如图,ABCD是圆O的内接正方形,E是劣弧CD上一点,EA交BD于F,EB交AC于G,且GF⊥AE.
如图,ABCD是圆O的内接正方形,E是劣弧CD上一点,EA交BD于F,EB交AC于G,且GF⊥AE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
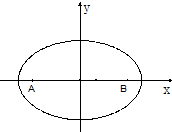 椭圆满足这样的光学性质:从椭圆的一个焦点发射的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.现有一个水平放置的椭圆形台球盘,满足方程$\frac{x^2}{64}+\frac{y^2}{28}=1$,点A,B是它的两个焦点.当静止的小球从点A开始出发,沿直线运动,经椭圆壁反射后再回到点A时,此时小球经过的路程可能是( )
椭圆满足这样的光学性质:从椭圆的一个焦点发射的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.现有一个水平放置的椭圆形台球盘,满足方程$\frac{x^2}{64}+\frac{y^2}{28}=1$,点A,B是它的两个焦点.当静止的小球从点A开始出发,沿直线运动,经椭圆壁反射后再回到点A时,此时小球经过的路程可能是( )| A. | 32或4或$16-4\sqrt{7}$ | B. | $16+4\sqrt{7}$或28或$16-4\sqrt{7}$ | ||
| C. | 28或4或$16+4\sqrt{7}$ | D. | 32或28或4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com