练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．在等比数列{an}中，a2和a18为方程x2+15x+16=0的两根，则a3a10a17等于（　　）
    A．-256B．64C．-64D．256

    分析 由已知得a2a18=a102=16，由此能求出a3a10a17=a103=43=64．

    解答 解：∵a2和a18为方程x2+15x+16=0的两根，
    ∴a2+a18=-15，
    则该数列的公比是负数．
    由已知得a2a18=a102=16，
    解得a10=4（舍去）或a10=-4．
    ∴a3a10a17=a103=（-4）3=-64．
    故选：C．

    点评 本题考查数列的三项之积的求法，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．若某空间几何体的三视图如图所示，根据图中数据，可得该几何体的表面积是（　　）
    A．4+20πB．16+12πC．16+16πD．16+20π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

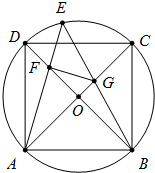    20．如图，ABCD是圆O的内接正方形，E是劣弧CD上一点，EA交BD于F，EB交AC于G，且GF⊥AE．
    （1）求证：AF•AE=AO•AC；
    （2）求证：$\frac{{2A{O^2}}}{{A{F^2}}}-\frac{FG}{AF}=1$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

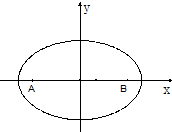    17．椭圆满足这样的光学性质：从椭圆的一个焦点发射的光线，经椭圆反射后，反射光线经过椭圆的另一个焦点．现有一个水平放置的椭圆形台球盘，满足方程$\frac{x^2}{64}+\frac{y^2}{28}=1$，点A，B是它的两个焦点．当静止的小球从点A开始出发，沿直线运动，经椭圆壁反射后再回到点A时，此时小球经过的路程可能是（　　）
    A．32或4或$16-4\sqrt{7}$B．$16+4\sqrt{7}$或28或$16-4\sqrt{7}$
    C．28或4或$16+4\sqrt{7}$D．32或28或4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知双曲线过点$（\sqrt{3}，4）$且渐近线方程为2x±y=0，则该双曲线的标准方程为$\frac{{y}^{2}}{4}-{x}^{2}$=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．5位顾客将各自的帽子放在衣架上，然后，每人随意取走一顶帽子，则没有一个人拿到自己帽子的概率为$\frac{11}{30}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知数列$\sqrt{2}，\sqrt{5}，2\sqrt{2}，\sqrt{11}$，…则$2\sqrt{17}$是它的第23项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．顶点在原点，对称轴是坐标轴，且经过点（4，-2）的抛物线方程是（　　）
    A．y2=xB．x2=-8yC．y2=-x或x2=8yD．y2=x或x2=-8y

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知函数f（x）=lnx，h（x）=ax（a∈R）．
    （I）函数f（x）与h（x）的图象无公共点，试求实数a的取值范围；
    （Ⅱ）是否存在实数m，使得对任意的x∈（$\frac{1}{2}$，+∞），都有函数y=f（x）+$\frac{m}{x}$的图象在g（x）=$\frac{{e}^{x}}{x}$的图象的下方？若存在，请求出最大整数m的值；若不存在，请说理由．
    （参考数据：ln2=0.6931，ln3=1.0986，$\sqrt{e}$=1.6487，$\root{3}{e}$=1.3956）．

    查看答案和解析>>

    同步练习册答案