
| A. | 21 | B. | 22 | C. | 23 | D. | 24 |
分析 由$\frac{{a}_{13}}{{a}_{12}}$<-1,可得$\frac{{a}_{13}+{a}_{12}}{{a}_{12}}<0$,由它们的前n项和Sn有最大可得a12>0,a13+a12<0,a13<0从而有a1+a23=2a12>0,a1+a24=a13+a12<0,从而可求满足条件的n的值.
解答 解:因为$\frac{{a}_{13}}{{a}_{12}}$<-1,可得$\frac{{a}_{13}+{a}_{12}}{{a}_{12}}<0$,由它们的前n项和Sn有最大值,可得数列的d<0
∴a12>0,a13+a12<0,a13<0
∴a1+a23=2a12>0,a1+a24=a13+a12<0,
使得Sn>0的n的最大值n=23
故选:C.
点评 本题主要考查了等差数列的性质在求解和的最值中应用,解题的关键是由已知及它们的前n项和Sn有最大,推出数列的正项是解决本题的关键点.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:解答题
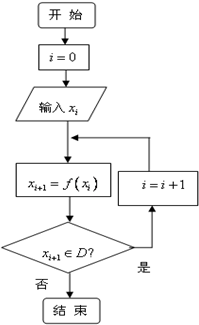 对任意函数f(x),x∈D,可按如图构造一个数列发生器,数列发生器产生数列{xn}.
对任意函数f(x),x∈D,可按如图构造一个数列发生器,数列发生器产生数列{xn}.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 等腰直角三角形 | C. | 直角三角形 | D. | 等腰三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com