
分析 (1)代入m值,求出导函数,根据导函数求出函数的单调区间和极值;
(2)求出函数的导函数,把恒成立问题转化为最值问题,根据导函数对参数m分类讨论,判断函数的最大值,使最大值小于等于零即可.
解答 (1)∵m=1时,f(x)=lnx-x2-x+1(x>0),
∴$f'(x)=\frac{1}{x}-2x-1=\frac{{-({2x-1})({x+1})}}{x}$,
∴$x∈({0,\frac{1}{2}}),f'(x)>0$;$x∈({\frac{1}{2},+∞})$,..,
∴f(x)的单调递增区间为$({0,\frac{1}{2}})$,单调递减区间为$({\frac{1}{2},+∞})$,f(x)的极大值秋$f({\frac{1}{2}})=\frac{1}{4}-ln2$,无极小值.
(2)∵f(x)=lnx-mx2+(1-2m)x+1(x>0),
∴$f'(x)=\frac{1}{x}-2mx+1-2m=\frac{{-2m{x^2}+({1-2m})x+1}}{x}$,
当m≤0时,f'(x)>0恒成立,f(x)单调递增,无最大值,
∵f(x)≤0恒成立,
∴不成立.
当m>0时,
∴$x∈({0,\frac{1}{2m}})$,f'(x)>0;$x∈({\frac{1}{2m},+∞}),f'(x)<0$,
∴f(x)在区间$({0,\frac{1}{2m}})$上单调递增区间$({\frac{1}{2m},+∞})$上单调递减,
f(x)的最大值为$f({\frac{1}{2m}})≤0$,即4mln2m≥1,
∵m∈Z,
∴显然,m=1时,4ln2≥1成立,
∴m的最小值为1.
点评 考查了导函数求函数的单调性和极值,对恒成立问题的转化和对参数的分类讨论.属于常规题型,应熟练掌握.


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
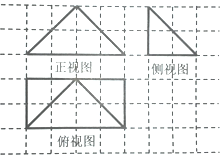 某几何体的三视图如图所示(网络中每个小正方形的边长为1),若这个几何体的顶点都在球O的表面上,则这个球的表面积是( )
某几何体的三视图如图所示(网络中每个小正方形的边长为1),若这个几何体的顶点都在球O的表面上,则这个球的表面积是( )| A. | 20π | B. | 4$\sqrt{5}$π | C. | $\frac{49π}{16}$ | D. | $\frac{49π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -i | B. | i | C. | 1+i | D. | 1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
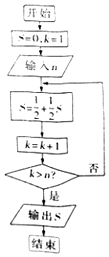
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com