
分析 (Ⅰ)当x∈(1,2]时,$f(x)=1+{log_{\frac{1}{3}}}x$,从而f($\sqrt{3}$)=$\frac{1}{2}$,由此能求出函数f(x)为二阶伸缩函数,由此能求出$f(2\sqrt{3})$的值.
(Ⅱ)当x∈(1,3]时,$f(x)=\sqrt{3x-{x^2}}$,由此推导出函数$y=f(x)-\sqrt{2}x$在(1,+∞)上无零点.
(Ⅲ)当x∈(kn,kn+1]时,$f(x)={k^n}f(\frac{x}{k^n})$,由此得到$f(\frac{x}{k^n})∈[0,1)$,当x∈(kn,kn+1]时,f(x)∈[0,kn),由此能求出f(x)在(0,kn+1](n∈N*)上的取值范围是[0,kn).
解答 解:(Ⅰ)由题设,当x∈(1,2]时,$f(x)=1+{log_{\frac{1}{3}}}x$,
∴$f(\sqrt{3})=1+lo{g_{\frac{1}{3}}}\sqrt{3}=1-\frac{1}{2}=\frac{1}{2}$.
∵函数f(x)为二阶伸缩函数,
∴对任意x∈(0,+∞),都有f(2x)=2f(x).
∴$f(2\sqrt{3})=2f(\sqrt{3})=1$.(4分)
(Ⅱ)当x∈(3m,3m+1](m∈N*)时,$\frac{x}{3^m}∈(1,3]$.
由f(x)为三阶伸缩函数,有f(3x)=3f(x).
∵x∈(1,3]时,$f(x)=\sqrt{3x-{x^2}}$.
∴$f(x)=3f(\frac{x}{3})={3^2}f(\frac{x}{3^2})=…={3^m}f(\frac{x}{3^m})={3^m}\sqrt{3•(\frac{x}{3^m})-{{(\frac{x}{3^m})}^2}}=\sqrt{{3^{m+1}}•x-{x^2}}$.
令$f(x)-\sqrt{2}x=0$,解得x=0或x=3m,它们均不在(3m,3m+1]内.(7分)
∴函数$y=f(x)-\sqrt{2}x$在(1,+∞)上无零点. (8分)
(Ⅲ) 由题设,若函数f(x)为k阶伸缩函数,有f(kx)=kf(x),
且当x∈(1,k]时,f(x)的取值范围是[0,1).
∴当x∈(kn,kn+1]时,$f(x)={k^n}f(\frac{x}{k^n})$.
∵$\frac{x}{k^n}∈(1,k]$,所以$f(\frac{x}{k^n})∈[0,1)$.
∴当x∈(kn,kn+1]时,f(x)∈[0,kn).
当x∈(0,1]时,即0<x≤1,
则?k(k≥2,k∈N*)使$0<\frac{1}{k}<x≤1$,
∴1<kx≤k,即kx∈(1,k],∴f(kx)∈[0,1).
又$f(x)=\frac{1}{k}f(kx)$,∴$f(x)=\frac{1}{k}f(kx)∈[0,\frac{1}{k})$,即$f(x)∈[0,\frac{1}{k})$.
∵k≥2,
∴f(x)在(0,kn+1](n∈N*)上的取值范围是[0,kn). (12分)
点评 本题考查函数值的求法,考查函数值无零点的证明,是中档题,解题时要认真审题,注意函数性质的合理运用.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:选择题
| A. | $\left\{{-1,\frac{1}{2}}\right\}$ | B. | {-1,0} | C. | $\left\{{-1,0,\frac{1}{2}}\right\}$ | D. | $\left\{{0,\frac{1}{2}}\right\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}x-y-2\sqrt{3}$-1=0 | B. | $\sqrt{3}x-3y-2\sqrt{3}$-3=0 | C. | $\sqrt{3}x-y+2\sqrt{3}$+1=0 | D. | $\sqrt{3}x-3y+2\sqrt{3}+3=0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
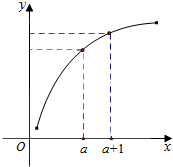
| A. | 0<f′(a)<f′(a+1)<f(a+1)-f(a) | B. | 0<f′(a+1)<f(a+1)-f(a)<f′(a) | ||
| C. | 0<f′(a+1)<f′(a)<f(a+1)-f(a) | D. | 0<f(a+1)-f(a)<f′(a)<f′(a+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1) | B. | (0,1) | C. | [1,3) | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{6}$ | B. | -6 | C. | 6 | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com