练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．过点（2，-1）且倾斜角为60°的直线方程为（　　）
    A．$\sqrt{3}x-y-2\sqrt{3}$-1=0B．$\sqrt{3}x-3y-2\sqrt{3}$-3=0C．$\sqrt{3}x-y+2\sqrt{3}$+1=0D．$\sqrt{3}x-3y+2\sqrt{3}+3=0$

    分析 由直线的倾斜角求出直线的斜率，代入直线方程的点斜式，整理为一般式得答案．

    解答 解：∵直线的倾斜角为60°，
    ∴斜率k=tan60°=$\sqrt{3}$，
    又直线过点（2，-1），
    由直线方程的点斜式得：y+1=$\sqrt{3}（x-2）$，
    化为一般式：$\sqrt{3}x-y-2\sqrt{3}-1=0$．
    故选：A．

    点评 本题考查直线的点斜式方程，考查了直线的倾斜角与斜率的关系，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    17．已知x3k=5，y2k=3，求x6k•y4k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．某校从2名男生和3名女生中随机选出3名学生做义工，则选出的学生中男女生都有的概率为$\frac{9}{10}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

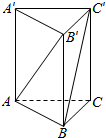    20．如图，在正三棱柱ABC-A′B′C′中，若AA′=2AB，则异面直线AB′与BC′所成角的余弦值为（　　）
    A．0B．$\frac{3}{8}$C．$\frac{3}{5}$D．$\frac{7}{10}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知定义在R上的奇函数f （x）满足f（x）=f（4-x），且在区间[0，2]上是增函数，那么（　　）
    A．f（6）＜f（4）＜f（1）B．f（4）＜f（6）＜f（1）C．f（1）＜f（6）＜f（4）D．f（6）＜f（1）＜f（4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．抛物线y2=2px（p＞0）与直线y=x+1相切，A（x1，y1），B（x2，y2）（x1≠x2）是抛物线上两个动点，F为抛物线的焦点，且|AF|+|BF|=8．
    （Ⅰ）求p的值；
    （Ⅱ） 线段AB的垂直平分线l与x轴的交点是否为定点，若是，求出交点坐标，若不是，说明理由；
    （Ⅲ）求直线l的斜率的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．定义在（0，+∞）上的函数f（x），如果对任意x∈（0，+∞），都有f（kx）=kf（x）（k≥2，k∈N*）成立，则称f（x）为k阶伸缩函数．
    （Ⅰ）若函数f（x）为二阶伸缩函数，且当x∈（1，2]时，$f（x）=1+{log_{\frac{1}{3}}}x$，求$f（2\sqrt{3}）$的值；
    （Ⅱ）若函数f（x）为三阶伸缩函数，且当x∈（1，3]时，$f（x）=\sqrt{3x-{x^2}}$，求证：函数$y=f（x）-\sqrt{2}x$在（1，+∞）上无零点；
    （Ⅲ）若函数f（x）为k阶伸缩函数，且当x∈（1，k]时，f（x）的取值范围是[0，1），求f（x）在（0，kn+1]（n∈N*）上的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．气象台预报“本市明天降雨概率是70%”，下列说法正确的是（　　）
    A．本市明天将有70%的地区降雨B．本市明天将有70%的时间降雨
    C．明天出行带雨具的可能性很大D．明天出行不带雨具肯定要淋雨

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知点$（a，\frac{1}{2}）$在幂函数f（x）=（a-1）xb的图象上，则函数f（x）是（　　）
    A．奇函数B．偶函数
    C．定义域内的减函数D．定义域内的增函数

    查看答案和解析>>

    同步练习册答案