
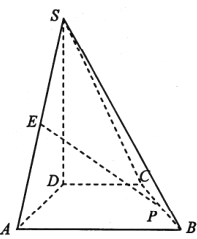
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 是直角梯形,
是直角梯形,![]() .
.
(1)求二面角![]() 的余弦值;
的余弦值;
(2)设![]() 是棱
是棱![]() 上一点,
上一点,![]() 是
是![]() 的中点,若
的中点,若![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)建立空间坐标系:则![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,![]() .设平面
.设平面![]() 的法向量为
的法向量为![]() ,由
,由![]() ,
,![]() ,得
,得![]() 且
且![]() .取
.取![]() ,得
,得![]() ,
,![]() ,
,
所以![]() 是平面
是平面![]() 的一个法向量.因为
的一个法向量.因为![]() 平面ABC,取平面ABC的一个法向量
平面ABC,取平面ABC的一个法向量![]() .设二面角
.设二面角![]() 的大小为
的大小为![]() ,所以
,所以![]() ,(2)由(1)知
,(2)由(1)知![]() ,则
,则![]() ,
,![]() .设
.设![]() (
(![]() ),则
),则![]() ,
,
所以![]() .易知
.易知![]() 平面
平面![]() ,所以
,所以![]() 是平面
是平面![]() 的一个法向量.设
的一个法向量.设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,所以
,所以![]() , 即
, 即![]()
试题解析:
(1)以D为坐标原点,建立如图所示空间
直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由![]() ,
,![]() ,得
,得![]() 且
且![]() .
.
取![]() ,得
,得![]() ,
,![]() ,
,
所以![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
因为![]() 平面ABC,取平面ABC的一个法向量
平面ABC,取平面ABC的一个法向量![]() .
.
设二面角![]() 的大小为
的大小为![]() ,所以
,所以![]() ,
,
由图可知二面角![]() 为锐二面角,所以二面角
为锐二面角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.
(2)由(1)知![]() ,则
,则![]() ,
,![]() .
.
设![]() (
(![]() ),则
),则![]() ,
,
所以![]() .
.
易知![]() 平面
平面![]() ,所以
,所以![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
所以![]() , 即
, 即![]() ,得
,得![]() 或
或![]() (舍).所以
(舍).所以![]() ,
,![]() ,所以线段
,所以线段![]() 的长为
的长为![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】一家公司计划生产某种小型产品的月固定成本为1万元,每生产1万件需要再投入2万元,设该公司一个月内生产该小型产品x万件并全部销售完,每万件的销售收入为4﹣x万元,且每万件国家给予补助2e﹣ ![]() ﹣
﹣ ![]() 万元.(e为自然对数的底数,e是一个常数)
万元.(e为自然对数的底数,e是一个常数)
(1)写出月利润f(x)(万元)关于月产量x(万件)的函数解析式
(2)当月产量在[1,2e]万件时,求该公司在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生成量值(万件).(注:月利润=月销售收入+月国家补助﹣月总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 a∈R,函数 f(x)=a﹣ ![]() .
.
(1)证明:f(x)在(﹣∞,+∞)上单调递增;
(2)若f(x)为奇函数,求:
①a的值;
②f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(﹣1,4)及圆C:(x﹣2)2+(y﹣3)2=1.则下列判断正确的序号为 .
①点P在圆C内部;
②过点P做直线l,若l将圆C平分,则l的方程为x+3y﹣11=0;
③过点P做直线l与圆C相切,则l的方程为y﹣4=0或3x+4y﹣13=0;
④一束光线从点P出发,经x轴反射到圆C上的最短路程为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项积为
项积为![]() ,即
,即![]() .
.
(1)若数列![]() 为首项为2016,公比为
为首项为2016,公比为![]() 的等比数列,
的等比数列,
①求![]() 的表达式;②当
的表达式;②当![]() 为何值时,
为何值时, ![]() 取得最大值;
取得最大值;
(2)当![]() 时,数列
时,数列![]() 都有
都有![]() 且
且![]() 成立,
成立,
求证: ![]() 为等比数列.
为等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,且其图象关于直线x=0对称,则( )
,且其图象关于直线x=0对称,则( )
A.y=f(x)的最小正周期为π,且在(0, ![]() )上为增函数
)上为增函数
B.y=f(x)的最小正周期为π,且在(0, ![]() )上为减函数
)上为减函数
C.y=f(x)的最小正周期为 ![]() ,且在
,且在 ![]() 上为增函数
上为增函数
D.y=f(x)的最小正周期为 ![]() ,且在
,且在 ![]() 上为减函数
上为减函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com