
分析 由数列递推式可得n≥2时有an=2Sn-1+2n-1,与原递推式联立可得${a}_{n+1}+{2}^{n}=3({a}_{n}+{2}^{n-1})$(n≥2),说明从第二项起,数列{${a}_{n}+{2}^{n-1}$}公差等比数列,由等比数列的通项公式求得数列{an}的通项公式.
解答 解:当n≥2时,由an+1=2Sn+2n,①
得an=2Sn-1+2n-1,②
两式作差可得:${a}_{n+1}-{a}_{n}=2({S}_{n}-{S}_{n-1})+{2}^{n}-{2}^{n-1}=2{a}_{n}+{2}^{n-1}$,
∴${a}_{n+1}+{2}^{n}=3({a}_{n}+{2}^{n-1})$(n≥2),
又a2=2a1+2=4,∴a2+2=6,
∴当n≥2时,${a}_{n}+{2}^{n-1}=6×{3}^{n-2}$,
则${a}_{n}=2×{3}^{n-1}-{2}^{n-1}$,
又2×31-1-21-1=1=a1,
∴${a}_{n}=2×{3}^{n-1}-{2}^{n-1}$.
故答案为:2×3n-1-2n-1.
点评 本题考查数列递推式,考查了等比关系的确定,训练了等比数列通项公式的求法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-∞,$\frac{1}{4}$) | C. | ($\frac{1}{4}$,+∞) | D. | (0,$\frac{1}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
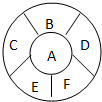 如图、用四种不同的颜色给标有字母的6个区域染色,要求相邻的区域不能染同色,则不同的染色方法有( )
如图、用四种不同的颜色给标有字母的6个区域染色,要求相邻的区域不能染同色,则不同的染色方法有( )| A. | 720种 | B. | 240种 | C. | 120种 | D. | 96种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 各侧面都是等腰三角形 | B. | 侧棱长度相等且底面是菱形 | ||
| C. | 所有棱长都相等 | D. | 底面是三角形且三条侧棱两两垂直 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com