
分析 (1)利用两角和差的正切公式求得 tanα 的值,再利用同角三角函数的基本关系求得要求式子的值.
(2)利用诱导公式、二倍角的正弦公式,求得sin$\frac{π}{12}$•sin$\frac{5π}{12}$的值.
解答 解:(1)∵已知tan($\frac{π}{4}$+α)=$\frac{1+tanα}{1-tanα}$=$\frac{1}{2}$,
∴tanα=-$\frac{1}{3}$,
∴$\frac{sinα-cosα}{sinα+cosα}$=$\frac{tanα-1}{tanα+1}$=-2.
(2)sin$\frac{π}{12}$•sin$\frac{5π}{12}$=sin$\frac{π}{12}$cos$\frac{π}{12}$=$\frac{1}{2}$sin$\frac{π}{6}$=$\frac{1}{4}$.
点评 本题主要考查同角三角函数的基本关系、两角和差的正切公式,诱导公式以及二倍角的正弦公式的应用,属于基础题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | xf(x)在(0,6)单调递减 | B. | xf(x)在(0,6)单调递增 | ||
| C. | xf(x)在(0,6)上有极小值2π | D. | xf(x)在(0,6)上有极大值2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
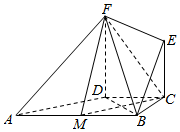 如图所示,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AF=BF,EC∥FD,FD⊥底面ABCD,M是AB的中点.
如图所示,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AF=BF,EC∥FD,FD⊥底面ABCD,M是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$$\overrightarrow a$+$\frac{1}{2}$$\overrightarrow b$ | B. | $\frac{1}{2}$$\overrightarrow a$+$\frac{1}{4}$$\overrightarrow b$ | C. | $\frac{2}{3}$$\overrightarrow a$+$\frac{1}{3}$$\overrightarrow b$ | D. | $\frac{1}{2}$$\overrightarrow a$+$\frac{2}{3}$$\overrightarrow b$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com