
| A. | xf(x)在(0,6)单调递减 | B. | xf(x)在(0,6)单调递增 | ||
| C. | xf(x)在(0,6)上有极小值2π | D. | xf(x)在(0,6)上有极大值2π |
分析 设g(x)=xf(x),得到g′(x)=[xf(x)]′=$\frac{sinx}{x}$,解关于导函数的不等式,求出函数的单调区间,得到函数的极大值,从而求出答案.
解答 解:∵x2f′(x)+xf(x)=sinx(x∈(0,6),
∴xf′(x)+f(x)=$\frac{sinx}{x}$,
设g(x)=xf(x),则g′(x)=[xf(x)]′=$\frac{sinx}{x}$,
由g′(x)>0,解得:0<x<π,g′(x)<0,解得:π<x<6,
∴x=π时,函数g(x)=xf(x)取得最大值g(π)=πf(π)=2π,
故选:D.
点评 本题考查了函数的单调性、极值问题,考查导数的应用,构造函数g(x)=xf(x)是解题的关键,本题是一道中档题.


 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
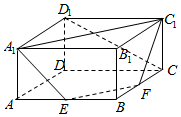 如图,在长方体ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E,F分别是棱AB,BC的中点.证明A1,C1,F,E四点共面,并求直线CD1与平面A1C1FE所成角的正弦值.
如图,在长方体ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E,F分别是棱AB,BC的中点.证明A1,C1,F,E四点共面,并求直线CD1与平面A1C1FE所成角的正弦值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125] |
| 频数 | 30 | 120 | 210 | 100 | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
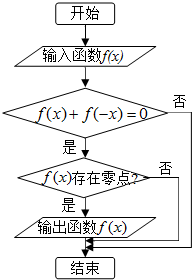
| A. | f(x)=xtanx | B. | f(x)=xex | C. | f(x)=x+2lnx | D. | f(x)=x-sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com