
分析 (1)①将二次函数配方,结合图象,可得开口方向、对称轴方程、顶点坐标;
②由顶点处取得最值,可得函数的最大值或最小值;
③结合图象和对称轴,可得单调性;
(2)考虑对称轴与区间的关系,判断单调性,即可得到所求范围.
解答 解:(1)①二次函数y=-4x2+8x-3,
即为y=-4(x-1)2+1,
函数图象的开口方向向下、对称轴方程为x=1、顶点坐标(1,1);
②当x=1时,函数的最大值为1,无最小值;
③函数f(x)在(-∞,1)递增,在(1,+∞)递减.
(2)x∈[-1,5),
f(x)在[-1,1)递增,在(1,5)递减,
可得f(1)取得最大值1,又f(-1)=-15,f(5)=-63.
则函数y的取值范围是(-63,1].
点评 本题考查二次函数的图象和性质,主要考查函数的最值和在闭区间上的值域,注意运用单调性,考虑对称轴和区间的关系,考查运算能力,属于基础题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:解答题
 为了解某高校学生中午午休时间玩手机情况,随机抽取了100名大学生进行调查.下面是根据调查结果绘制的学生日均午休时间的频率分布直方图:将日均午休时玩手机不低于40分钟的学生称为“手机控”.
为了解某高校学生中午午休时间玩手机情况,随机抽取了100名大学生进行调查.下面是根据调查结果绘制的学生日均午休时间的频率分布直方图:将日均午休时玩手机不低于40分钟的学生称为“手机控”.| 非手机迷 | 手机迷 | 合计 | |
| 男 | x | x | m |
| 女 | y | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| P(k2≥x0) | 0.05 | 0.10 |
| k0 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{7}{3}π+3kπ,-\frac{1}{6}π+3kπ}],k∈Z$ | B. | $[{-\frac{5}{3}π+3kπ,-\frac{1}{6}π+3kπ}],k∈Z$ | ||
| C. | $[{-\frac{2}{3}π+2kπ,-\frac{1}{6}π+2kπ}],k∈Z$ | D. | $[{-\frac{1}{3}π+2kπ,-\frac{1}{6}π+2kπ}],k∈Z$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
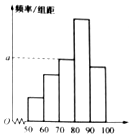 某教师为了分析所任教班级某将考试的成绩,将全班同学的成绩做出了频数与频率的统计表和频率分布直方图.
某教师为了分析所任教班级某将考试的成绩,将全班同学的成绩做出了频数与频率的统计表和频率分布直方图.| 分组 | 频数 | 频率 |
| [50,60) | 3 | 0.06 |
| [60,70) | m | 0.10 |
| [70,80) | 13 | n |
| [80,90) | p | q |
| [90,100] | 9 | 0.18 |
| 总计 | t | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∈R,x<0 | B. | ¬p:?x∈R,x≤0 | C. | ¬p:?x∈R,x<0 | D. | ¬p:?x∈R,x≤0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com