
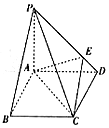
 如图,点P是边长为1的正方形ABCD所在平面外一点,PA⊥CD,PA=1,PD=$\sqrt{2}$,E为PD上一点,PE=2ED.
如图,点P是边长为1的正方形ABCD所在平面外一点,PA⊥CD,PA=1,PD=$\sqrt{2}$,E为PD上一点,PE=2ED.分析 (1)根据勾股定理的逆定理,得到△PAD是以PD为斜边的直角三角形,从而有PA⊥AD,再结合PA⊥CD,AD、CD 相交于点D,可得PA⊥平面ABCD;
(2)以AB,AD,PA为x轴、y轴、z轴建立空间直角坐标系.分别给出点A、B、C、P、E的坐标,从而得出$\overrightarrow{AC}$=(1,1,0),$\overrightarrow{AE}$=(0,$\frac{2}{3}$,$\frac{1}{3}$),利用向量数量积为零的方法,列方程组可算出平面AEC的一个法向量.假设侧棱PC上存在一点F,使得BF∥平面AEC,则$\overrightarrow{BF}$?$\overrightarrow{n}$=0,解之得存在PC的中点F,使得BF∥平面AEC.
解答 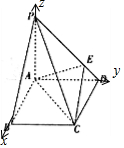 (1)证明:∵PA=AD=1,PD=$\sqrt{2}$,
(1)证明:∵PA=AD=1,PD=$\sqrt{2}$,
∴PA2+AD2=PD2,可得△PAD是以PD为斜边的直角三角形
∴PA⊥AD
又∵PA⊥CD,AD、CD 相交于点D,
∴PA⊥平面ABCD;
(2)解:以AB,AD,PA为x轴、y轴、z轴建立空间直角坐标系.
则A(0,0,0),B(1,0,0),C(1,1,0),P(0,0,1),E(0,$\frac{2}{3}$,$\frac{1}{3}$),
$\overrightarrow{AC}$=(1,1,0),$\overrightarrow{AE}$=(0,$\frac{2}{3}$,$\frac{1}{3}$),
设平面AEC的法向量$\overrightarrow{n}$=(x,y,z),根据数量积为零,可得$\left\{\begin{array}{l}{x+y=0}\\{2y+z=0}\end{array}\right.$
令y=1,得$\overrightarrow{n}$=(-1,1,-2 )
假设侧棱PC上存在一点F,且$\overrightarrow{CF}$=λ$\overrightarrow{CP}$,(0≤λ≤1),使得:BF∥平面AEC,则$\overrightarrow{BF}$?$\overrightarrow{n}$=0.
又∵$\overrightarrow{BF}$=(0,1,0)+(-λ,-λ,λ)=(-λ,1-λ,λ),
∴$\overrightarrow{BF}$?$\overrightarrow{n}$=λ+1-λ-2λ=0,∴λ=$\frac{1}{2}$,
所以存在PC的中点F,使得BF∥平面AEC.
点评 本题给出一个特殊的棱锥,着重考查了直线与平面平行的判定与性质和直线与平面垂直的判定与性质等知识点,属于中档题.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:解答题
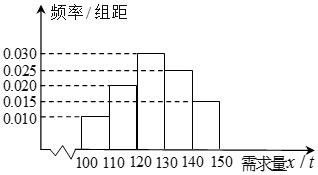 随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x≠0,则x2-3x≠0”的否命题是“若x=0,则x2-3x=0” | |
| B. | 命题“?x∈R,lg(x2-x+1)≥0”是假命题 | |
| C. | 命题“?x∈R,3sinx=$\sqrt{3}$”是真命题 | |
| D. | 命题“若x=1,则向量$\overrightarrow{a}$=(-2x,1)与$\overrightarrow{b}$=(-2,x)共线”的逆命题是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 蒜台 | 4吨 | 1.2万元 | 0.55万元 |
| 花菜 | 6吨 | 0.9万元 | 0.3万元 |
| A. | 50万 | B. | 48万 | C. | 47万 | D. | 45万 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | [-3,+∞) | C. | [-3,0] | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com