考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(Ⅰ)f(x)存在两个极值点,等价于其导函数有两个相异零点;
(Ⅱ)先找出(x1-x2)的取值范围,再利用g(x)的导函数可找出最小值;
(Ⅲ)适当构造函数,并注意x1与x2的关系,转化为函数求最大值问题,证明相关不等式.
解答:
解:(Ⅰ)由题:
f′(x)=2x+(x>-2)∵函数f(x)存在两个极值点x
1、x
2,且x
1<x
2∴关于x的方程
2x+=0即2x
2+4x+a=0在(-2,+∞)内有不等二实根
令S(x)=2x
2+4x(x>-2)、T(x)=-a,则
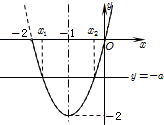
由图象可得-2<-a<0即0<a<2
∴实数a的取值范围是(0,2).
(Ⅱ)由(Ⅰ)可知
,
∴x
1-x
2=x
1-(-2-x
1)=2x
1+2,
∴-2<x
1-x
2<0,
由g(x)=xe
x得g'(x)=(x+1)e
x,
∴当x∈(-2,-1)时,g'(x)<0,即g(x)在(-2,-1)单调递减;
当x∈(-1,0)时,g'(x)>0,即g(x)在(-1,0)单调递增;
∴
g(x1-x2)min=g(-1)=-;
(Ⅲ)由(Ⅰ)知
,
∴
==x2+-2(x2+2)ln(-x2)+4,
令-x
2=x,则0<x<1且
=-x-+2(x-2)lnx+4,
令
F(x)=-x-+2(x-2)lnx+4(0<x<1),则
F′(x)=-1++2lnx+=-+2lnx+1(0<x<1),
∴
F″(x)=-++=,
∵0<x<1,
∴F''(x)<0即F'(x)在(0,1)上是减函数,
∴F'(x)>F'(1)=1>0,
∴F(x)在(0,1)上是增函数,
∴F(x)<F(1)=-1即
<-1.
点评:本题考查导函数,函数的单调性,最值,不等式证明,考查学生分析解决问题的能力,属于中档题.



