
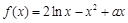 (
(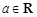 ).
).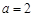 时,求
时,求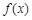 的图象在
的图象在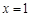 处的切线方程;
处的切线方程;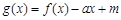 在
在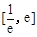 上有两个零点,求实数
上有两个零点,求实数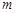 的取值范围;
的取值范围;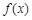 的图象与
的图象与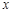 轴有两个不同的交点
轴有两个不同的交点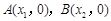 ,且
,且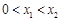 ,求证:
,求证: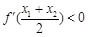 (其中
(其中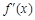 是
是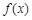 的导函数).
的导函数).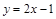 ;(2)
;(2)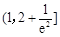 ;(3)证明见解析.
;(3)证明见解析.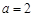 时,
时, ,
,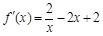 ,切点坐标为
,切点坐标为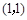 ,
,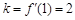 ,则切线方程为
,则切线方程为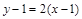 ,即
,即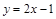 .
.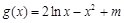 ,则
,则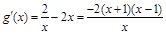 ,
,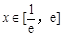 ,故
,故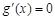 时,
时,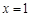 .当
.当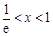 时,
时,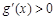 ;当
;当 时,
时, .
.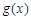 在
在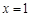 处取得极大值
处取得极大值 .
.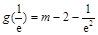 ,
,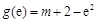 ,
,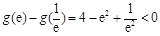 ,则
,则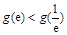 ,
,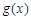 在
在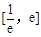 上有两个零点,则
上有两个零点,则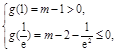
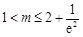 ,即实数
,即实数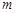 的取值范围是
的取值范围是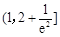 .
. 的图象与
的图象与 轴交于两个不同的点
轴交于两个不同的点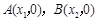 ,
,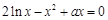 的两个根为
的两个根为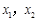 ,则
,则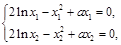 两式相减得
两式相减得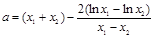 .又
.又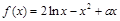 ,
,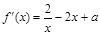 ,则
,则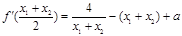
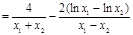 .
.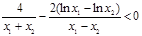 (*),即证明
(*),即证明 ,
,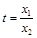 ,
,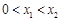 ,∴
,∴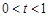 ,即证明
,即证明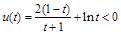 在
在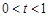 上恒成立.
上恒成立.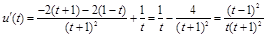 ,又
,又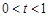 ,∴
,∴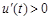 ,
,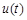 在
在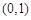 上是增函数,则
上是增函数,则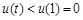 ,从而知
,从而知 ,
,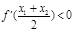 成立.
成立.

 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源:不详 题型:解答题
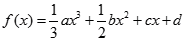 的图像过原点,且在点
的图像过原点,且在点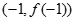 处的切线与
处的切线与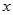 轴平行,对任意
轴平行,对任意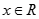 ,都有
,都有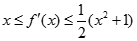 .
.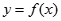 在点
在点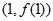 处切线的斜率;
处切线的斜率;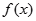 的解析式;
的解析式;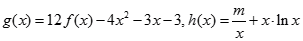 ,对任意
,对任意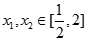 ,都有
,都有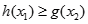 .求实数
.求实数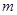 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com