
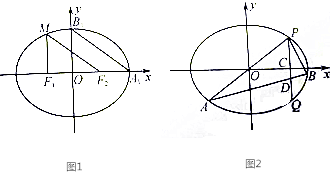
���� ��1������֪������Բ�����г������飬���a��b���ɴ��������Բ�ķ��̣�
��2�����ֱ��AD�ķ��̣�������Բ�ķ��̣������������B�����֤꣬��kPA•kPB��-1�����ɵõ�ֱ��PA��PB����ֱ��
��� �⣺��1������ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ���ֱ�ΪF1��-c��0����F2��c��0����
��2��2e����eΪ��ԲE�������ʣ�����Բ�ϣ���A1��B1�ֱ�Ϊ��Բ���Ҷ�����϶��㣬
����Բ��һ��M��x�������ߣ�����Ϊ����F1����MF2��A1B1��
��$\left\{\begin{array}{l}{\frac{4}{{a}^{2}}+\frac{4{e}^{2}}{{b}^{2}}=1}\\{\frac{\frac{{b}^{2}}{a}}{b}=\frac{2c}{a}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$�����a=$\sqrt{5}$��b=2��c=1��
����ԲE�ķ���Ϊ$\frac{{x}^{2}}{5}+\frac{{y}^{2}}{4}=1$��
��2��PA��PB����ֱ��
֤������P��x0��y0������A��-x0��-y0����D��x0��-$\frac{{y}_{0}}{3}$������$\frac{{{x}_{0}}^{2}}{5}+\frac{{{y}_{0}}^{2}}{4}$=1��
��ֱ��AD�ķ���y=$\frac{{y}_{0}}{3{x}_{0}}$��x+x0��-y0������Բ�ķ��̣�
�������ã�36x02+5${{y}_{0}}^{2}$��x2-20x0y02x+20x02y02-180x02=0��
�����⣬��֪�˷��̱���һ��-x0��
xB=$\frac{20{x}_{0}{{y}_{0}}^{2}}{36{{x}_{0}}^{2}+5{{y}_{0}}^{2}}$+x0��yB=$\frac{{y}_{0}}{3{x}_{0}}$��$\frac{20{x}_{0}{{y}_{0}}^{2}}{36{{x}_{0}}^{2}+5{{y}_{0}}^{2}}$+2x0��-y0=$\frac{5{{y}_{0}}^{3}-12{{x}_{0}}^{2}{y}_{0}}{36{{x}_{0}}^{2}+5{{y}_{0}}^{2}}$��
��kPB=$\frac{\frac{5{{y}_{0}}^{3}-12{{x}_{0}}^{2}{y}_{0}}{36{{x}_{0}}^{2}+5{{y}_{0}}^{2}}-{y}_{0}}{\frac{20{x}_{0}{{y}_{0}}^{2}}{36{{x}_{0}}^{2}+5{{y}_{0}}^{2}}}$=-$\frac{12}{5}•\frac{{x}_{0}}{{y}_{0}}$��
����kPA•kPB=-$\frac{12}{5}$����PA��PB����ֱ��
���� ���⿼��ֱ���������ߵ�λ�ù�ϵ��������Բ�ķ��̣�����ֱ������Բ��λ�ù�ϵ������Τ�ﶨ�������ã������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{3}��^2}{4}$-1 | B�� | $\frac{3��^2}{4}$-1 | C�� | $\frac{3��^2}{16}$-1 | D�� | $\frac{��^2}{2}$-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com