
分析 (I)由题意可设抛物线的标准方程为:y2=2px(p>0),由$\frac{p}{2}$=1,解得p即可得出.
(2)设A$(\frac{{y}_{1}^{2}}{4},{y}_{1})$,B$(\frac{{y}_{2}^{2}}{4},{y}_{2})$,由四边形ACBF为平行四边形,可得$\overrightarrow{FC}$=$\overrightarrow{FA}+\overrightarrow{FB}$,可得$\overrightarrow{OC}$,把点C坐标代入抛物线W方程可得:y1y2=-2.直线l的方程为:(y-y1)(y1+y2)=4x-${y}_{1}^{2}$,令y=0,解得x为定值.
(III)设直线l的方程为:my=x-$\frac{1}{2}$,A(x1,y1),B(x2,y2),与抛物线方程联立化为:y2-4my-2=0,可得|AB|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$,点F到直线l的距离d=$\frac{1}{2\sqrt{1+{m}^{2}}}$.S平行四边形ACBF=$2×\frac{1}{2}$d|AB|,再利用二次函数的性质即可得出.
解答 (I)解:由题意可设抛物线的标准方程为:y2=2px(p>0).
∵焦点为F(1,0),∴$\frac{p}{2}$=1,解得p=2.
∴抛物线W的标准方程为y2=4x.
(2)证明:设A$(\frac{{y}_{1}^{2}}{4},{y}_{1})$,B$(\frac{{y}_{2}^{2}}{4},{y}_{2})$,
$\overrightarrow{FA}$=$(\frac{{y}_{1}^{2}}{4}-1,{y}_{1})$,$\overrightarrow{FB}$=$(\frac{{y}_{2}^{2}}{4}-1,{y}_{2})$.
∵四边形ACBF为平行四边形,
∴$\overrightarrow{FC}$=$\overrightarrow{FA}+\overrightarrow{FB}$=$(\frac{{y}_{1}^{2}+{y}_{2}^{2}}{4}-2,{y}_{1}+{y}_{2})$,
∴$\overrightarrow{OC}$=$\overrightarrow{OF}$+$(\frac{{y}_{1}^{2}+{y}_{2}^{2}}{4}-2,{y}_{1}+{y}_{2})$=$(\frac{{y}_{1}^{2}+{y}_{2}^{2}}{4}-1,{y}_{1}+{y}_{2})$,
∵点C在抛物线W上,∴$({y}_{1}+{y}_{2})^{2}$=4$(\frac{{y}_{1}^{2}+{y}_{2}^{2}}{4}-1)$,
化为:y1y2=-2.
直线l的方程为:y-y1=$\frac{{y}_{1}-{y}_{2}}{\frac{{y}_{1}^{2}-{y}_{2}^{2}}{4}}$$(x-\frac{{y}_{1}^{2}}{4})$,
化为:(y-y1)(y1+y2)=4x-${y}_{1}^{2}$,
令y=0,可得:-y1y2=4x,∴2=4x,解得x=$\frac{1}{2}$.
∴直线l经过定点$(\frac{1}{2},0)$.y1+y2=0时也成立.
∴直线l恒经过定点$(\frac{1}{2},0)$.
(III)解:设直线l的方程为:my=x-$\frac{1}{2}$,A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{my=x-\frac{1}{2}}\\{{y}^{2}=4x}\end{array}\right.$,化为:y2-4my-2=0,
∴y1+y2=4m,y1y2=-2.
∴|AB|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$=$\sqrt{(1+{m}^{2})(16{m}^{2}+8)}$=2$\sqrt{(1+{m}^{2})[4{m}^{2}+2]}$.
点F到直线l的距离d=$\frac{\frac{1}{2}}{\sqrt{1+{m}^{2}}}$=$\frac{1}{2\sqrt{1+{m}^{2}}}$.
∴S平行四边形ACBF=$2×\frac{1}{2}$d|AB|=$\frac{1}{2\sqrt{1+{m}^{2}}}$×2$\sqrt{(1+{m}^{2})[4{m}^{2}+2]}$=$\sqrt{4{m}^{2}+2}$≥$\sqrt{2}$,当且仅当m=0时取等号.
∴l⊥x轴时,四边形ACBF面积的最小值为$\sqrt{2}$.
点评 本题考查了抛物线的标准方程及其性质、直线与抛物线相交弦长问题、点到直线的距离公式、三角形面积计算公式、二次函数的单调性,考查了推理能力与计算能力,属于难题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
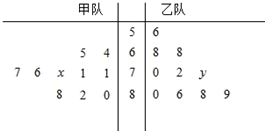 如图的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分),已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.
如图的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分),已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com