
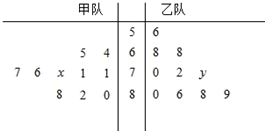
 如图的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分),已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.
如图的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分),已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.分析 (1)甲代表队的中位数为76,结合茎叶图能求出x的值;乙代表队的平均数为75,结合茎叶图能求出y的值.
(2)分别求出甲、乙的平均数和方差,由此得到甲队成绩较为稳定.
解答 解:(1)因为甲代表队的中位数为76,
其中已知高于76的有77,80,82,88,
低于76的有71,71,65,64,
所以x=6,…(3分)
因为乙代表队的平均数为75,
其中超过75的差值为5,11,13,14,和为43,
少于75的差值为3,5,7,7,19,和为41,
所以y=3.…(6分)
(2)∵${\bar x_甲}=\frac{1}{10}$(64+65+71+71+76+76+77+80+82+88)=75,…(8分)
乙代表队数据的平均数是75.
∴${S^2}_甲=\frac{1}{10}$[(64-75)2+(65-75)2+…+(88-75)2]=50.2…(9分)
又S2乙=$\frac{1}{10}$[(56-75)2+(68-75)2+…+(89-75)2]=70.3…(10分)
∴${S^2}_甲<{S^2}_乙$,
∴甲队成绩较为稳定.…(12分)
点评 本题考查茎叶图的应用,考查中位数、平均数、方差的求法及应用,是基础题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧(¬q)是真命题 | B. | (¬p)∨q是真命题 | C. | p∧q是假命题 | D. | p∨q是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 线段 | B. | 双曲线的一支 | C. | 圆 | D. | 射线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com