
分析 ①利用抽象函数的关系进行递推即可.
②根据函数单调性的定义,利用定义法进行证明即可,
③利用作差法结合抽象函数的关系进行证明即可.
解答 证明:①∵f(m)=f(n•$\frac{m}{n}$)=f($\frac{m}{n}$)+f(n),
∴f($\frac{m}{n}$)=f(m)-f(n);
②任取x1,x2∈(0,+∞),且x1<x2,则$f({x_2})-f({x_1})=f(\frac{x_2}{x_1})$,
∵x1<x2,∴$\frac{x_2}{x_1}>1$,
∴$f(\frac{x_2}{x_1})>0∴f({x_2})>f({x_1})$,
∴f(x)在(0,+∞)上是增函数.
③f($\frac{m+n}{2}$)-$\frac{f(m)+f(n)}{2}$=$\frac{1}{2}$f($\frac{m+n}{2}$)+$\frac{1}{2}$f($\frac{m+n}{2}$)-$\frac{f(m)+f(n)}{2}$
=$\frac{1}{2}$(f($\frac{m+n}{2}$)-f(m))+$\frac{1}{2}$(f($\frac{m+n}{2}$)-f(n))
=$\frac{1}{2}$f($\frac{m+n}{2m}$)+$\frac{1}{2}$f($\frac{m+n}{2m}$)=$\frac{1}{2}$f($\frac{(m+n)^{2}}{4{m}^{2}}$),
∵$\frac{{{{(m+n)}^2}}}{{4{m^2}}}≥1∴f[\frac{{{{(m+n)}^2}}}{{4{m^2}}}]≥0$
故$f(\frac{m+n}{2})≥$$\frac{f(m)+f(n)}{2}$.
点评 本题主要考查抽象函数的应用,根据抽象函数的关系结合函数单调性的定义是解决本题的关键.考查学生的运算和推理能力.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:解答题
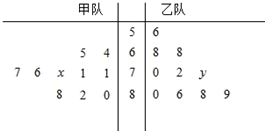 如图的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分),已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.
如图的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分),已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {0,1,2,3} | C. | {-1,0,1,2} | D. | {-1,0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-1,+∞) | C. | [1,+∞) | D. | (-∞,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com