
分析 利用函数的解析式分别求解函数值,然后利用结果,猜想结论.
解答 解:$f(x)=\frac{1}{{1+{2^x}}}-1$,则f(1)+f(-1)=$\frac{1}{3}$-1+$\frac{1}{1+\frac{1}{2}}$-1=-1;
f(2)+f(-2)=$\frac{1}{1+4}$-1+$\frac{1}{1+\frac{1}{4}}$-1=-1;
f(3)+f(-3)=$\frac{1}{1+9}$-1+$\frac{1}{1+\frac{1}{9}}$-1=-1;
可以提出猜想:f(n)+f(-n)=-1.(n∈N+).
故答案为:-1;-1;-1;f(n)+f(-n)=-1.(n∈N+).
点评 本题考查函数值的求法,归纳推理的应用,考查计算能力.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,已知点A(-2,0),B(2,0),动点C满足条件:△ABC的周长为10,记动点C的轨迹为曲线M.
在平面直角坐标系xOy中,已知点A(-2,0),B(2,0),动点C满足条件:△ABC的周长为10,记动点C的轨迹为曲线M.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
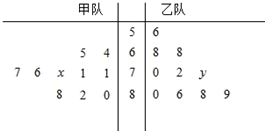 如图的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分),已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.
如图的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分),已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com