
在某市组织的一次数学竞赛中全体参赛学生的成绩近似服从正态分布N(60,100),已知成绩在90分以上(含90分)的学生有13人.
(1)求此次参加竞赛的学生总数共有多少人?
(2)若计划奖励竞赛成绩排在前228名的学生,问受奖学生的分数线是多少?
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标模块练习卷(解析版) 题型:填空题
某次知识竞赛规则如下:在主办方预设的5个问题中,选手若能连续正确回答出两个问题,即停止答题,晋级下一轮.假设某选手正确回答每个问题的概率都是0.8,且每个问题的回答结果相互独立,则该选手恰好回答了4个问题就晋级下一轮的概率等于________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标3.2练习卷(解析版) 题型:填空题
由一组样本数据(x1,y1),(x2,y2),…,(xn,yn)得到线性回归方程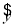 =
=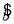 x+
x+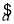 ,那么下列说法正确的是________.
,那么下列说法正确的是________.
①直线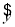 =
=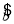 x+
x+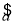 必经过点(
必经过点(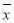 ,
, );
);
②直线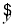 =
=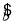 x+
x+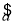 至少经过点(x1,y1),(x2,y2),…,(xn,yn)中的一个点;
至少经过点(x1,y1),(x2,y2),…,(xn,yn)中的一个点;
③直线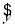 =
=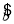 x+
x+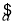 的斜率为
的斜率为 ;
;
④直线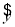 =
=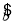 x+
x+ 和各点(x1,y1),(x2,y2),…,(xn,yn)的偏差
和各点(x1,y1),(x2,y2),…,(xn,yn)的偏差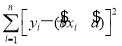 是该坐标平面上的直线与这些点的最小偏差.
是该坐标平面上的直线与这些点的最小偏差.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2章练习卷(解析版) 题型:填空题
设两个正态分布N(μ1,σ12)(σ1>0)和N(μ2,σ22)(σ2>0)的密度函数图象如图所示,则有μ1与μ2,σ1与σ2的大小关系是________.
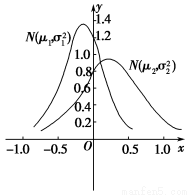
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2章练习卷(解析版) 题型:填空题
如图,EFGH是以O为圆心,半径为1的圆内接正方形.将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在正方形EFGH内”,B表示事件“豆子落在扇形OHE(阴影部分)内”,则(1)P(A)=________;
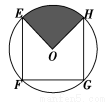
(2)P(B|A)=________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.6练习卷(解析版) 题型:填空题
对于正态分布N(0,1)的概率密度函数P(x)=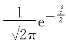 ,有下列四种说法:①P(x)为偶函数;②P(x)的最大值为
,有下列四种说法:①P(x)为偶函数;②P(x)的最大值为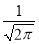 ;③P(x)在x>0时是单调减函数,在x≤0时是单调增函数;④P(x)关于σ=1对称.不正确的是________(填序号).
;③P(x)在x>0时是单调减函数,在x≤0时是单调增函数;④P(x)关于σ=1对称.不正确的是________(填序号).
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.5练习卷(解析版) 题型:解答题
甲、乙两名射手各打了10发子弹,其中甲击中环数与次数如下表
环数 | 5 | 6 | 7 | 8 | 9 | 10 |
次数 | 1 | 1 | 1 | 1 | 2 | 4 |
乙射击的概率分布列如表
环数 | 7 | 8 | 9 | 10 |
概率 | 0.2 | 0.3 | p | 0.1 |
(1)若甲,乙两人各打一枪,求共击中18环的概率及p的值;
(2)比较甲,乙两人射击水平的优劣.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.5练习卷(解析版) 题型:填空题
投掷两个骰子,至少有一个4点或5点出现时,就说这次试验成功,则在10次试验中,成功次数X的期望是________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.3练习卷(解析版) 题型:填空题
设A、B是两个事件,0<P(A)<1,P(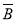 |A)=1.
|A)=1.
则下列结论:①P(AB)=0;②P(A+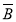 )=P(A);
)=P(A);
③P(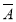 )=P(B);④P(A)=P(
)=P(B);④P(A)=P(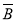 ).其中正确的是________.
).其中正确的是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com