Question

17．如图，在四棱椎P-ABCD中，底面ABCD是边长为6的菱形，侧棱PD⊥平面ABCD，BD=6，PD=3$\sqrt{6}$，点E，F分别是PB，CB上靠近点B的一个三等分点．
（Ⅰ）求证：AC⊥DE；
（Ⅱ）求三棱椎F-PAB的高；
（Ⅲ）在线段PC上是否存在一点G，使得FG与平面PDC所成角的正弦值为$\frac{1}{3}$？若存在，请求出CG的长，若不存在，请说明理由．

Answer 1

分析 （Ⅰ）证明AC⊥平面PBD，即可证明AC⊥DE；
（Ⅱ）由V_{三棱锥F-PAB}=V_{三棱锥P-ABF}，求出三棱椎F-PAB的高；
（Ⅲ）假设在线段PC上存在一点G，使FG与平面PDC所成角的正弦值为$\frac{1}{3}$，得出点G不在线段PC上．

解答 解：（Ⅰ）证明：四棱椎P-ABCD中，底面ABCD是菱形，
∴AC⊥BD，
又PD⊥平面ABCD，AC?平面ABCD，
∴PD⊥AC，
又PD∩BD=D，
PD?平面PBD，BD?平面PBD，
∴AC⊥平面PBD，
又DE?平面PBD，
∴AC⊥DE；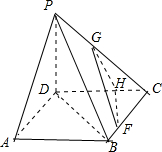
（Ⅱ）∵V_{三棱锥F-PAB}=V_{三棱锥P-ABF}，
∴$\frac{1}{3}$S_△PAB•h=$\frac{1}{3}$S_△ABF•PD，
∴h=$\frac{{S}_{△ABF}•PD}{{S}_{△PAB}}$=$\frac{\frac{1}{6}×\frac{1}{2}×6×6\sqrt{3}×3\sqrt{6}}{\frac{1}{2}×6×\sqrt{{（6\sqrt{2}）}^{2}{-3}^{2}}}$=$\frac{3\sqrt{14}}{7}$；
∴三棱椎F-PAB的高为$\frac{3\sqrt{14}}{7}$；
（Ⅲ）设在线段PC上存在一点G，使FG与平面PDC所成角的正弦值为$\frac{1}{3}$，
如图所示；
则过点F作FH⊥DC于H，连接GH，
∵PD⊥平面ABCD，PD?平面PCD，
∴平面PCD⊥平面ABCD；
又平面PCD∩平面ABCD=CD，
∴FH⊥平面PCD，
∴∠FGH是直线GF与平面PCD所成的角；
又GH?平面PCD，∴HF⊥GH；
∵FC=$\frac{2}{3}$BC=4，
∴HF=FCsin$\frac{π}{3}$=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$，
HC=FCcos$\frac{π}{3}$=4×$\frac{1}{2}$=2；
∵sin∠FGH=$\frac{HF}{FG}$=$\frac{1}{3}$，
∴FG=3HF=3×2$\sqrt{3}$=6$\sqrt{3}$，
∴HG=$\sqrt{{GF}^{2}{-HF}^{2}}$=$\sqrt{{（6\sqrt{3}）}^{2}{-（2\sqrt{3}）}^{2}}$=4$\sqrt{6}$＞6=PC，
∴点G不在线段PC上．

点评 本题考查了空间中垂直关系的判断与应用问题，也考查了用等积法求锥体高的应用问题，考查了空间想象能力与逻辑思维能力，是综合性问题．