
| A. | $(\frac{4}{3},2)$ | B. | $[\frac{4}{3},2)$ | C. | $(-∞,\frac{4}{3})∪(2,+∞)$ | D. | $(-∞,\frac{4}{3}]∪(2,+∞)$ |
分析 根据一元二次方程与一元二不等式的关系求出a,b的值,带入再求解不等式$\frac{a(x-1)}{x+b}$≥6的解.
解答 解:不等式ax2+bx+2>0的解集为(-$\frac{1}{2}$,$\frac{1}{3}$),
可得:一元二次方程ax2+bx+2=0的根:${x}_{1}=-\frac{1}{2}$,${x}_{2}=\frac{1}{3}$,
由韦达定理:可得:$\left\{\begin{array}{l}{\frac{2}{a}=-\frac{1}{6}}\\{-\frac{b}{a}=\frac{1}{3}-\frac{1}{2}}\end{array}\right.$,
解得:a=-12,b=-2.
∴不等式$\frac{a(x-1)}{x+b}$≥6化简得:$\frac{2(1-x)}{x-2}≤1$等价于(4-3x)(x-2)≤0,且x-2≠0,
解得:$\frac{4}{3}≤x<2$.
故选:B.
点评 本题考查不等式的解法,一元二次方程与一元二不等式的关系,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
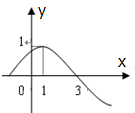 函数f(x)=sin(ωx+φ),(x∈R,ω>0,0<φ<π)的部分图象如图所示,则( )
函数f(x)=sin(ωx+φ),(x∈R,ω>0,0<φ<π)的部分图象如图所示,则( )| A. | $ω=\frac{π}{2},φ=\frac{π}{4}$ | B. | $ω=\frac{π}{3},φ=\frac{π}{6}$ | C. | $ω=\frac{π}{4},φ=\frac{π}{4}$ | D. | $ω=\frac{π}{4},φ=\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | ($\frac{5}{2}$,+∞) | C. | (2,$\frac{5}{2}$) | D. | [2,$\frac{5}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1008 | B. | 1010 | C. | $\frac{2019}{2}$ | D. | 2019 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (∁RF)∪G | B. | ∁R(F∩G) | C. | F∩G | D. | (∁RF)∩(∁RG) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-a,-f(a)) | B. | (0,0) | C. | (a,f(-a)) | D. | (-a,-f(-a)) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com