
| A. | (∁RF)∪G | B. | ∁R(F∩G) | C. | F∩G | D. | (∁RF)∩(∁RG) |
分析 不等式f(x)≥0的解集为F,可得f(x)<0的解集为${C}_{R}^{\;}$F,不等式g(x)<0的解集为G,可得g(x)≥0的解集为${C}_{R}^{\;}G$,不等式组的解集,就是其交集.可得答案.
解答 解:由题意:函数f(x),g(x)的定义域为R,不等式f(x)≥0的解集为F.
∴f(x)<0的解集为${C}_{R}^{\;}$F,
不等式g(x)<0的解集为G,
∴g(x)≥0的解集为${C}_{R}^{\;}G$,
所以不等式组$\left\{\begin{array}{l}{f(x)<0}\\{g(x)≥0}\end{array}\right.$的解集为(∁RF)∩(∁RG).
故选D.
点评 本题考查不等式的解法,转化思想,不等式组实质是不等式的交集.属于基础题.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
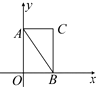 已知Rt△ABC的三边长分别为AB=5,BC=4,AC=3,在平面直角坐标系中,△ABC的初始位置如图(图中CB⊥x轴),现将△ABC沿x轴滚动,设点A(x,y)的轨迹方程是y=f(x),则f(2017)=( )
已知Rt△ABC的三边长分别为AB=5,BC=4,AC=3,在平面直角坐标系中,△ABC的初始位置如图(图中CB⊥x轴),现将△ABC沿x轴滚动,设点A(x,y)的轨迹方程是y=f(x),则f(2017)=( )| A. | $\sqrt{21}$ | B. | $2\sqrt{6}$ | C. | 4 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{4}{3},2)$ | B. | $[\frac{4}{3},2)$ | C. | $(-∞,\frac{4}{3})∪(2,+∞)$ | D. | $(-∞,\frac{4}{3}]∪(2,+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (-∞,-1)∪(2,+∞) | C. | (-2,1) | D. | (-∞,-2)∪(1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com