
| A. | 1008 | B. | 1010 | C. | $\frac{2019}{2}$ | D. | 2019 |
分析 由f(x)=$\frac{x+1}{2x-1}$,则f(1-x)=$\frac{1-x+1}{2(1-x)-1}$=$\frac{x-2}{2x-1}$,可知f(x)+f(1-x)=$\frac{x+1}{2x-1}$+$\frac{x-2}{2x-1}$=1,采用倒叙相加法求得求得前2016项和,由a2017=f(1)=2,则S2017=S2016+a2017,即可求得的S2017值.
解答 解:f(x)=$\frac{x+1}{2x-1}$,则f(1-x)=$\frac{1-x+1}{2(1-x)-1}$=$\frac{x-2}{2x-1}$,
∴f(x)+f(1-x)=$\frac{x+1}{2x-1}$+$\frac{x-2}{2x-1}$=1,
∵an=f($\frac{n}{2017}$),
a2017=f(1)=2
∴a1+a2016=f($\frac{1}{2017}$)+f($\frac{2016}{2017}$)=1,
∴a2+a2015=1,
…
a2016+a1=1
S2016=a1+a2+a3+…+a2016,
S2016=a2016+a2015+a2014+…+a1,
∴2S2016=(a1+a2016)+(a2+a2015)+…+(a2016+a1),
∴S2016=1008,
S2017=S2016+a2017=1008+f(1)=1010,
故选B.
点评 本题考查数列与函数的综合应用,考查倒叙相加法求数列的前n项和,考查计算能力,对于此类题应该构造f(x)+f(1-x)=常数,再利用倒叙相加法即可求得,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-2,5] | B. | [-2,2] | C. | [-1,2] | D. | [-2,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,三棱锥P-ABC中,PA⊥底面ABC,AB=AC=AP=1,BC=$\sqrt{2}$,D是BC的中点,则图中直角三角形的个数是8.
如图,三棱锥P-ABC中,PA⊥底面ABC,AB=AC=AP=1,BC=$\sqrt{2}$,D是BC的中点,则图中直角三角形的个数是8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
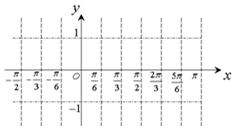 已知函数f(x)=cos(2x-$\frac{π}{3}$)+2sin(x-$\frac{π}{4}$)sin(x+$\frac{π}{4}$).
已知函数f(x)=cos(2x-$\frac{π}{3}$)+2sin(x-$\frac{π}{4}$)sin(x+$\frac{π}{4}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{4}{3},2)$ | B. | $[\frac{4}{3},2)$ | C. | $(-∞,\frac{4}{3})∪(2,+∞)$ | D. | $(-∞,\frac{4}{3}]∪(2,+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}-\sqrt{2}}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com