在△ABC中.角A.B.C的对边分别为a.b.c.若a=2.A=45°.C=75°.则b等于( )A．$\frac{{\sqrt{6}-\sqrt{2}}}{2}$B．$\sqrt{3}$C．$\frac{{\sqrt{6}}}{2}$D．$\sqrt{6}$ 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

17．在△ABC中，角A，B，C的对边分别为a，b，c，若a=2，A=45°，C=75°，则b等于（　　）

A．

$\frac{{\sqrt{6}-\sqrt{2}}}{2}$

B．

$\sqrt{3}$

C．

$\frac{{\sqrt{6}}}{2}$

D．

$\sqrt{6}$

分析由已知利用三角形内角和定理可求B，进而利用正弦定理即可得解b的值．

解答解：∵A=45°，C=75°，a=2，
∴B=180°-A-C=60°，
∴b=$\frac{asinB}{sinA}$=$\frac{2×\frac{\sqrt{3}}{2}}{\frac{\sqrt{2}}{2}}$=$\sqrt{6}$．
故选：D．

点评本题主要考查了三角形内角和定理，正弦定理在解三角形中的应用，考查了转化思想，属于基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

7．

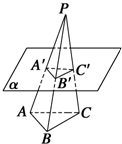如图所示，P是三角形ABC所在平面外一点，平面α∥平面ABC，α分别交线段PA、PB、PC于A′、B′、C′，若PA′：AA′=3：4，则S_{△A′B′C′}：S_△ABC=9：49．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

8．已知函数f（x）=$\frac{x+1}{2x-1}$，数列{a_n}的前n项和为S_n，且a_n=f（$\frac{n}{2017}$），则S₂₀₁₇=（　　）

A．

1008

B．

1010

C．

$\frac{2019}{2}$

D．

2019

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

5．

某研究所计划利用“神十”宇宙飞船进行新产品搭载实验，计划搭载若干件新产品A、B，该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生的收益来决定具体搭载安排，有关数据如下表：

	每件产品A	每件产品B
研制成本、搭载费用之和（万元）	20	30	计划最大资金额 300万元
产品重量（千克）	10	5	最大搭载重量110千克
预计收益（万元）	80	60

分别用x，y表示搭载新产品A，B的件数．总收益用Z表示
（Ⅰ）用x，y列出满足生产条件的数学关系式，并画出相应的平面区域；
（Ⅱ）问分别搭载新产品A、B各多少件，才能使总预计收益达到最大？并求出此最大收益．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

12．若函数y=f（x）为奇函数，则它的图象必经过点（　　）

A．

（-a，-f（a））

B．

（0，0）

C．

（a，f（-a））

D．

（-a，-f（-a））

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

2．给出下列结论：
①在△ABC中，sinA＞sinB?a＞b；
②常数数列既是等差数列又是等比数列；
③数列{a_n}的通项公式为${a_n}={n^2}-kn+1$，若{a_n}为递增数列，则k∈（-∞，2]；
④△ABC的内角A，B，C满足sinA：sinB：sinC=3：5：7，则△ABC为锐角三角形．其中正确结论的个数为（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

9．

如图，为了测量对岸A，B两点的距离，沿河岸选取C，D两点，测得CD=2km，∠CDB=∠ADB=30°，∠ACD=60°，∠ACB=45°，求A，B两点的距离．