
 Ρ≥―–ΨΩΥυΦΤΜ°άϊ”ΟΓΑ…ώ °Γ±”ν÷φΖ…¥§Ϋχ–––¬≤ζΤΖ¥ν‘Ί Β―ιΘ§ΦΤΜ°¥ν‘Ί»τΗ…Φΰ–¬≤ζΤΖAΓΔBΘ§ΗΟΥυ“ΣΗυΨίΗΟ≤ζΤΖΒΡ―–÷Τ≥…±ΨΓΔ≤ζΤΖ÷ΊΝΩΓΔ¥ν‘Ί Β―ιΖ―”ΟΚΆ‘ΛΦΤ≤ζ…ζΒΡ ’“φά¥ΨωΕ®ΨΏΧε¥ν‘ΊΑ≤≈≈Θ§”–ΙΊ ΐΨί»γœ¬±μΘΚ
Ρ≥―–ΨΩΥυΦΤΜ°άϊ”ΟΓΑ…ώ °Γ±”ν÷φΖ…¥§Ϋχ–––¬≤ζΤΖ¥ν‘Ί Β―ιΘ§ΦΤΜ°¥ν‘Ί»τΗ…Φΰ–¬≤ζΤΖAΓΔBΘ§ΗΟΥυ“ΣΗυΨίΗΟ≤ζΤΖΒΡ―–÷Τ≥…±ΨΓΔ≤ζΤΖ÷ΊΝΩΓΔ¥ν‘Ί Β―ιΖ―”ΟΚΆ‘ΛΦΤ≤ζ…ζΒΡ ’“φά¥ΨωΕ®ΨΏΧε¥ν‘ΊΑ≤≈≈Θ§”–ΙΊ ΐΨί»γœ¬±μΘΚ| ΟΩΦΰ≤ζΤΖA | ΟΩΦΰ≤ζΤΖB | ||
| ―–÷Τ≥…±ΨΓΔ¥ν‘Ί Ζ―”Ο÷°ΚΆΘ®Άρ‘ΣΘ© | 20 | 30 | ΦΤΜ°Ήν¥σΉ ΫπΕν 300Άρ‘Σ |
| ≤ζΤΖ÷ΊΝΩΘ®«ßΩΥΘ© | 10 | 5 | Ήν¥σ¥ν‘Ί÷ΊΝΩ110«ßΩΥ |
| ‘ΛΦΤ ’“φΘ®Άρ‘ΣΘ© | 80 | 60 |
Ζ÷Έω Θ®ΔώΘ©”…Χβ“βΘ§Ν–≥ωΙΊ”ΎxΘ§yΒΡ≤ΜΒ» ΫΉιΘ§”…≤ΜΒ» ΫΉιΒΟΒΫΤΫΟφ«χ”ρΦ¥Ω…ΘΜ
Θ®ΔρΘ©Ν–≥ωΡΩ±ξΚ· ΐΘ§ΗυΨίΘ®ΔώΘ©ΒΡ‘Φ χΧθΦΰ“‘ΦΑΩ…––”ρΘ§ΫαΚœΡΩ±ξΚ· ΐΒΡΦΗΚΈ“β“ε«σΉν¥σ÷ΒΦ¥Ω…Θ°
Ϋβ¥π ΫβΘΚΘ®ΔώΘ©ΫβΘΚ”…“―÷ΣxΘ§y¬ζΉψΒΡ ΐ―ßΙΊœΒ ΫΈΣ$\left\{{\begin{array}{l}{20x+30yΓή300}\\{10x+5yΓή110}\\{xΓί0}\\{yΓί0}\end{array}}\right.$Θ§«“xΓ NΘ§yΓ NΘ§
ΗΟΕΰ‘Σ“Μ¥Έ≤ΜΒ» ΫΉιΥυ±μ ΨΒΡ«χ”ρΈΣΆΦ÷–ΒΡ“θ”Α≤ΩΖ÷Θ° Γ≠Θ®6Ζ÷Θ©
Γ≠Θ®6Ζ÷Θ©
Θ®ΔρΘ©ΫβΘΚ…ηΉν¥σ ’“φΈΣzΆρ‘ΣΘ§‘ρΡΩ±ξΚ· ΐz=80x+60yΘ°
Ής≥ω÷±œΏlaΘΚ4x+3y=0≤ΔΤΫ“ΤΘ§”…ΆΦœσ÷ΣΘ§
Β±÷±œΏΨ≠ΙΐMΒψ ±Θ§zΡή»ΓΒΫΉν¥σ÷ΒΘ§
”…$\left\{{\begin{array}{l}{2x+3y=30}\\{2x+y=22}\end{array}}\right.$ΫβΒΟ$\left\{{\begin{array}{l}{x=9}\\{y=4}\end{array}}\right.$«“¬ζΉψxΓ NΘ§yΓ NΘ§Φ¥MΘ®9Θ§4Θ© «Ήν”≈ΫβΘ§
Υυ“‘zmax=80ΓΝ9+60ΓΝ4=960Θ®Άρ‘ΣΘ©Θ§
¥πΘΚ¥ν‘ΊA≤ζΤΖ9ΦΰΘ§B≤ζΤΖ4ΦΰΘ§Ρή ΙΉή‘ΛΦΤ ’“φ¥οΒΫΉν¥σ÷ΒΘ§Ήν¥σ‘ΛΦΤ ’“φΈΣ960Άρ‘ΣΘ°Γ≠Θ®12Ζ÷Θ©
ΒψΤά ±ΨΧβΩΦ≤ιΝΥΦρΒΞœΏ–‘ΙφΜ°Έ ΧβΒΡΫβΨω ’“φΉν¥σΘΜΙΊΦϋ «’ΐ»ΖΝ–≥ω‘Φ χΧθΦΰ“‘ΦΑΡΩ±ξΚ· ΐΘ§άϊ”Ο ΐ–ΈΫαΚœΒΡΖΫΖ®«σΉν÷ΒΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | y=$\frac{x}{2}$+$\frac{8}{x}$ | BΘ° | y=sinx+$\frac{4}{sinx}$Θ®0ΘΦxΘΦΠ–Θ© | ||
| CΘ° | y=ex+4e-x | DΘ° | y=$\sqrt{{x}^{2}+1}$+$\frac{2}{\sqrt{{x}^{2}+1}}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
 “―÷ΣΚ· ΐfΘ®xΘ©=cosΘ®2x-$\frac{Π–}{3}$Θ©+2sinΘ®x-$\frac{Π–}{4}$Θ©sinΘ®x+$\frac{Π–}{4}$Θ©Θ°
“―÷ΣΚ· ΐfΘ®xΘ©=cosΘ®2x-$\frac{Π–}{3}$Θ©+2sinΘ®x-$\frac{Π–}{4}$Θ©sinΘ®x+$\frac{Π–}{4}$Θ©Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 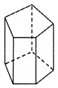 | BΘ° |  | CΘ° |  | DΘ° | 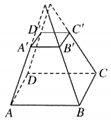 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | ΔΌΔΎΔέΔή | BΘ° | ΔΌΔΎΔέ | CΘ° | ΔέΔή | DΘ° | ΔΎΔή |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $\frac{{\sqrt{6}-\sqrt{2}}}{2}$ | BΘ° | $\sqrt{3}$ | CΘ° | $\frac{{\sqrt{6}}}{2}$ | DΘ° | $\sqrt{6}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com