
| A. | y=$\frac{x}{2}$+$\frac{8}{x}$ | B. | y=sinx+$\frac{4}{sinx}$(0<x<π) | ||
| C. | y=ex+4e-x | D. | y=$\sqrt{{x}^{2}+1}$+$\frac{2}{\sqrt{{x}^{2}+1}}$ |
分析 根据基本不等式的口诀:一正二定三相等,对各个选项逐一化简判断即可.
解答 解:A、当x>0时,$\frac{x}{2}+\frac{8}{x}$≥2$\sqrt{\frac{x}{2}•\frac{8}{x}}$=4,当且仅当$\frac{x}{2}=\frac{8}{x}$时取等号,
当x<0时,$\frac{x}{2}+\frac{8}{x}$≤-4,当且仅当$\frac{x}{2}=\frac{8}{x}$时取等号,A错误;
B、当0<x<π时,sinx>0,y=sinx+$\frac{4}{sinx}$≥2$\sqrt{sinx•\frac{4}{sinx}}$=4,
当且仅当sinx=$\frac{4}{sinx}$时取等号,此时sinx=2,由sinx≤1知,B不正确;
C、y=ex+4e-x≥2$\sqrt{{e}^{x}•4{e}^{-x}}$=4,
当且仅当ex=4e-x,即ex=2时取最小值4,C正确;
D、y=$\sqrt{{x}^{2}+1}+\frac{2}{\sqrt{{x}^{2}+1}}$≥2$\sqrt{\sqrt{{x}^{2}+1}•\frac{2}{\sqrt{{x}^{2}+1}}}$=$2\sqrt{2}$,
当且仅当$\sqrt{{x}^{2}+1}=\frac{2}{\sqrt{{x}^{2}+1}}$时取等号,函数的最小值是$2\sqrt{2}$,D错误.
故选:C.
点评 本题考查了基本不等式在求最值中的应用,牢记“一正二定三相等”是解题的关键,考查了化简、变形能力.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 或-2 | B. | 2 | C. | -2 | D. | -1或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -ln(e+1) | B. | -ln(4+e) | C. | -1 | D. | -ln(e+$\frac{1}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
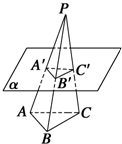 如图所示,P是三角形ABC所在平面外一点,平面α∥平面ABC,α分别交线段PA、PB、PC于A′、B′、C′,若PA′:AA′=3:4,则S△A′B′C′:S△ABC=9:49.
如图所示,P是三角形ABC所在平面外一点,平面α∥平面ABC,α分别交线段PA、PB、PC于A′、B′、C′,若PA′:AA′=3:4,则S△A′B′C′:S△ABC=9:49.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某研究所计划利用“神十”宇宙飞船进行新产品搭载实验,计划搭载若干件新产品A、B,该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生的收益来决定具体搭载安排,有关数据如下表:
某研究所计划利用“神十”宇宙飞船进行新产品搭载实验,计划搭载若干件新产品A、B,该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生的收益来决定具体搭载安排,有关数据如下表:| 每件产品A | 每件产品B | ||
| 研制成本、搭载 费用之和(万元) | 20 | 30 | 计划最大资金额 300万元 |
| 产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
| 预计收益(万元) | 80 | 60 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com