
分析 利用“1的饱和函数”的定义构造方程,判断方程是否有解,可得结论.
解答 解:①f(x)=2x,D=R,则存在实数x0,使得2x0+1=2x0+2,解得x0=1,
因为此方程有实数解,
所以函数f(x)=2x是“1的饱和函数”.
②f(x)=$\frac{1}{x}$,D=(-∞,0)∪(0,+∞),
若f(x)=$\frac{1}{x}$是“1的饱和函数”,
则存在非零实数x0,使得$\frac{1}{{x}_{0}+1}$=$\frac{1}{{x}_{0}}$+1,
即x02+x0+1=0,
因为此方程无实数解,
所以函数f(x)=$\frac{1}{x}$不是“1的饱和函数”.
③f(x)=lg(x2+2),若存在x,使f(x+1)=f(x)+f(1)
则lg[(x+1)2+2]=lg(x2+2)+lg3
即2x2-2x+3=0,
∵△=4-24=-20<0,故方程无解.
即f(x)=lg(x2+2)不是“1的饱和函数”.
④f(x)=cosπx,存在x=$\frac{1}{3}$,使得f(x+1)=cos$\frac{4}{3}$π=-$\frac{1}{2}$=f(x)+f(1)=cos$\frac{1}{3}$π+cosπ=$\frac{1}{2}-1$,
即f(x)=cosπx是“1的饱和函数”.
故答案:①④
点评 本题考查“1的饱和函数”的判断,是基础题,解题时要注意函数的性质的合理运用.


科目:高中数学 来源: 题型:解答题
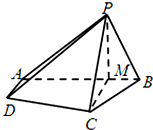 在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,点M是线段AB上的一点,且PM⊥CD,AB=BC=2PB=2AD=4BM.
在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,点M是线段AB上的一点,且PM⊥CD,AB=BC=2PB=2AD=4BM.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$f($\frac{π}{4}$)<$\sqrt{2}$f($\frac{π}{3}$) | B. | $\sqrt{3}$f($\frac{π}{4}$)>$\sqrt{2}$f($\frac{π}{3}$) | C. | $\sqrt{3}$f($\frac{π}{4}$)<$\sqrt{2}$f($\frac{π}{6}$) | D. | f($\frac{π}{4}$)>$\sqrt{2}$f($\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{x}{2}$+$\frac{8}{x}$ | B. | y=sinx+$\frac{4}{sinx}$(0<x<π) | ||
| C. | y=ex+4e-x | D. | y=$\sqrt{{x}^{2}+1}$+$\frac{2}{\sqrt{{x}^{2}+1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ①②③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com