
分析 直接由等差数列的通项公式和等差数列的性质逐一判断得答案.
解答 解:∵等差数列{an}的前n项和Sn能取到最大值,
∴数列{an}是递减数列,且d<0,故①正确;
${S}_{n}=n{a}_{1}+\frac{n(n-1)d}{2}=\frac{d}{2}{n}^{2}+({a}_{1}-\frac{d}{2})n$,∵d<0,∴数列{Sn}先增后减,故②错误;
由a10+a11<0,a10•a11<0,得a10>0,a11<0,
∴数列{Sn}的最大项是S10,故③正确;
由S19=19a10>0,${S}_{20}=\frac{({a}_{10}+{a}_{11})20}{2}<0$,得数列{Sn}的最小的正数是S19,故④正确.
∴正确的序号是①③④.
故答案为:①③④.
点评 本题考查了等差数列的通项公式,考查了等差数列的性质,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{x}{2}$+$\frac{8}{x}$ | B. | y=sinx+$\frac{4}{sinx}$(0<x<π) | ||
| C. | y=ex+4e-x | D. | y=$\sqrt{{x}^{2}+1}$+$\frac{2}{\sqrt{{x}^{2}+1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,三棱锥P-ABC中,PA⊥底面ABC,AB=AC=AP=1,BC=$\sqrt{2}$,D是BC的中点,则图中直角三角形的个数是8.
如图,三棱锥P-ABC中,PA⊥底面ABC,AB=AC=AP=1,BC=$\sqrt{2}$,D是BC的中点,则图中直角三角形的个数是8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
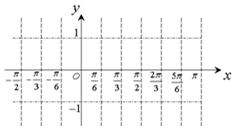 已知函数f(x)=cos(2x-$\frac{π}{3}$)+2sin(x-$\frac{π}{4}$)sin(x+$\frac{π}{4}$).
已知函数f(x)=cos(2x-$\frac{π}{3}$)+2sin(x-$\frac{π}{4}$)sin(x+$\frac{π}{4}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com