Question

18．设m，n∈R，定义在区间[m，n]上函数f（x）=x²的值域是[0，4]，若关于t的方程|3^-|t|-$\frac{1}{4}$|-n=0恰有4个互不相等的实数解，则m+n的取值范围是$（{-2，-\frac{7}{4}}）$．

Answer 1

分析 画出函数y=|3^-|t|-$\frac{1}{4}$|的图象，由关于t的方程|3^-|t|-$\frac{1}{4}$|-n=0恰有4个互不相等的实数解，求出n的范围，再由定义在区间[m，n]上函数f（x）=x²的值域是[0，4]，求出m值，可得答案．

解答 解：函数y=|3^-|t|-$\frac{1}{4}$|的图象如下图所示：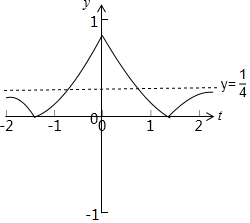

若关于t的方程|3^-|t|-$\frac{1}{4}$|-n=0恰有4个互不相等的实数解，
则n∈（0，$\frac{1}{4}$），
∵定义在区间[m，n]上函数f（x）=x²的值域是[0，4]，
∴m=-2，
故m+n∈$（{-2，-\frac{7}{4}}）$，
故答案为：$（{-2，-\frac{7}{4}}）$

点评 本题考查的知识点是函数的图象，方程根的个数，数形结合思想，二次函数的图象和性质，难度中档．