
【题目】某市实验中学数学教研组,在高三理科一班进行了一次“采用两种不同方式进行答卷”的考试实验,第一种做卷方式:按从前往后的顺序依次做;第二种做卷方式:先做简单题,再做难题.为了比较这两种做卷方式的效率,选取了![]() 名学生,将他们随机分成两组,每组
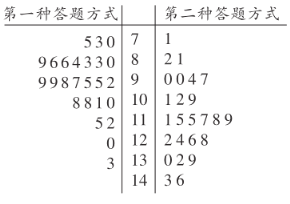
名学生,将他们随机分成两组,每组![]() 人.第一组学生用第一种方式,第二组学生用第二种方式,根据学生的考试分数(单位:分)绘制了茎叶图如图所示.
人.第一组学生用第一种方式,第二组学生用第二种方式,根据学生的考试分数(单位:分)绘制了茎叶图如图所示.
![]() 若
若![]() 分(含
分(含![]() 分)以上为优秀,根据茎叶图估计两种做卷方式的优秀率;
分)以上为优秀,根据茎叶图估计两种做卷方式的优秀率;
![]() 设
设![]() 名学生考试分数的中位数为
名学生考试分数的中位数为![]() ,根据茎叶图填写下面的
,根据茎叶图填写下面的![]() 列联表:
列联表:
超过中位数 | 不超过中位数 | 合计 | |
第一种做卷方式 | |||
第一种做卷方式 | |||
合计 |
根据列联表,能否有![]() 的把握认为两种做卷方式的效率有差异?
的把握认为两种做卷方式的效率有差异?
附: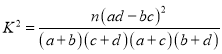 ,
,![]() .
.
|
|
|
|
|
|
|
|
【答案】![]() 第一种做卷方式的优秀率为
第一种做卷方式的优秀率为![]() ;第二种做卷方式的优秀率为
;第二种做卷方式的优秀率为![]() ;
;![]() 填表见解析;有
填表见解析;有![]() 的把握认为两种做卷方式的效率有差异.
的把握认为两种做卷方式的效率有差异.
【解析】
![]() 根据概率的计算方法运算即可;
根据概率的计算方法运算即可;
![]() 先算出中位数,代入数据算出
先算出中位数,代入数据算出![]() 的值,比较数据,得出结论.
的值,比较数据,得出结论.
解:![]() 根据茎叶图中的数据知,
根据茎叶图中的数据知,
用第一种做卷方式答卷的分数在![]() 分(含
分(含![]() 分)以上的有
分)以上的有![]() 人,
人,
![]() 第一种做卷方式的优秀率为
第一种做卷方式的优秀率为![]()
用第二种做卷方式答卷的分数在![]() 分(含
分(含![]() 分)以上的有
分)以上的有![]() 人,
人,
![]() 第二种做卷方式的优秀率为
第二种做卷方式的优秀率为![]() ;
;
![]() 这50名学生的考试分数按从小到大的顺序排列后,排在中间的两个数据是
这50名学生的考试分数按从小到大的顺序排列后,排在中间的两个数据是![]() 和
和![]() ,
,
则它们的中位数为![]() ;
;
由此填写列联表如下:
超过中位数 | 不超过中位数 | 合计 | |
第一种做卷方式 |
|
|
|
第一种做卷方式 |
|
|
|
合计 |
|
|
|
![]()
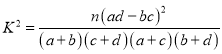
![]() ,
,
故![]() 的把握认为两种做卷方式的效率有差异.
的把握认为两种做卷方式的效率有差异.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,左顶点为
,左顶点为![]() ,且
,且![]() ,
,![]() 是椭圆上一点.
是椭圆上一点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 别与
别与![]() 轴交于点
轴交于点![]() ,求证:在
,求证:在![]() 轴上存在点
轴上存在点![]() ,使得无论非零实数
,使得无论非零实数![]() 怎样变化,以
怎样变化,以![]() 为直径的圆都必过点
为直径的圆都必过点![]() ,并求出点
,并求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次比赛中,某队的六名队员均获得奖牌,共获得4枚金牌2枚银牌,在颁奖晚会上,这六名队员与1名领队排成一排合影,若两名银牌获得者需站在领队的同侧,则不同的排法共有______种.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() ,
,![]() 分别是曲线
分别是曲线![]() ,
,![]() 上两动点且
上两动点且![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
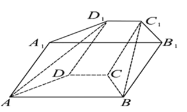
【题目】如图,在四棱柱![]() 中,底面
中,底面![]() 是等腰梯形,
是等腰梯形,![]() ,顶点
,顶点![]() 在底面
在底面![]() 内的射影恰为点
内的射影恰为点![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)若直线![]() 与底面
与底面![]() 所成的角为
所成的角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
:![]() ,点
,点![]() ,
,![]() ,点
,点![]() 在圆
在圆![]() 上,
上,![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 点在
点在![]() 轴上方),点
轴上方),点![]() 是抛物线
是抛物线![]() 上的动点,点
上的动点,点![]() 为
为![]() 的外心,求线段
的外心,求线段![]() 长度的最大值,并求出当线段
长度的最大值,并求出当线段![]() 长度最大时,
长度最大时,![]() 外接圆的标准方程.
外接圆的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有7个球,其中红色球2个(同色不加区分),白色,黄色,蓝色,紫色,灰色球各1个,将它们排成一行,要求最左边不排白色,2个红色排一起,黄色和红色不相邻,则有________种不同的排法(用数字回答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个不透明的盒子中装有4个大小、形状、手感完全相同的小球,分别标有数字1,2,3,4.现每次有放回地从中任意取出一个小球,直到标有偶数的球都取到过就停止.小明用随机模拟的方法估计恰好在第4次停止摸球的概率,利用计算机软件产生随机数,每1组中有4个数字,分别表示每次摸球的结果,经随机模拟产生了以下21组随机数:由此可以估计恰好在第4次停止摸球的概率为( )
1314 1234 2333 1224 3322 1413 3124 4321 2341 2413 1224 2143 4312
2412 1413 4331 2234 4422 3241 4331 4234
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com