
| A. | $\frac{64}{3}$ | B. | $\frac{32}{3}$ | C. | $\frac{64}{3}$或32 | D. | $\frac{32}{3}$或$\frac{64}{3}$ |
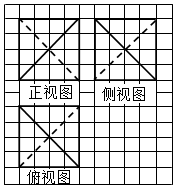
分析 由三视图知该几何体正四面体或五面体,且是棱长为2的正方体的一部分,画出直观图后,由正方体的性质求出该多面体的体积.
解答 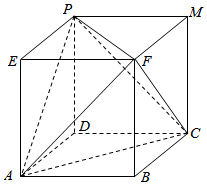 解由三视图知该几何体为正四面体P-ACF或几何体PFADC,
解由三视图知该几何体为正四面体P-ACF或几何体PFADC,
直观图如图所示:
则正四面体P-ACF是棱长为4的正方体的一部分,
由正方体的性质得,
三棱锥F-ABC的体积V三棱锥F-ABC=$\frac{1}{3}×\frac{1}{2}×4×4×4$=$\frac{32}{3}$,
∴正四面体P-ACF的体积V=4×4×4-4•V三棱锥F-ABC
=64-4×$\frac{32}{3}$=$\frac{64}{3}$,
该多面体的体积V=4×4×4-3•V三棱锥F-ABC
=64-3×$\frac{32}{3}$=32,
∴该多面体的体积为$\frac{64}{3}$或32,
故选C.
点评 本题考查三视图求几何体的体积,由三视图正确复原几何体是解题的关键,考查空间想象能力.


科目:高中数学 来源: 题型:解答题
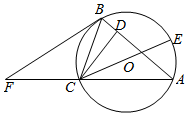 如图,已知AB=AC,圆O是△ABC的外接圆,CD⊥AB,CE是圆O的直径.过点B作圆O的切线交AC的延长线于点F.
如图,已知AB=AC,圆O是△ABC的外接圆,CD⊥AB,CE是圆O的直径.过点B作圆O的切线交AC的延长线于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一几何体的三视图如图所示,若将该几何体切割成长方体,则长方体的最大体积与该几何体的体积之比为( )
一几何体的三视图如图所示,若将该几何体切割成长方体,则长方体的最大体积与该几何体的体积之比为( )| A. | $\frac{2}{3}$ | B. | $\frac{36}{41}$ | C. | $\frac{18}{23}$ | D. | $\frac{9}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
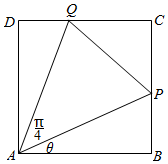 如图,某房产开发商计划在一正方形土地ABCD内建造一个三角形住宅区,在其余土地种植绿化,住宅区形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知,∠PAQ=$\frac{π}{4}$,设∠PAB=θ,记绿化率L=1-$\frac{△PAQ面积}{正方形ABCD面积}$,若L越大,则住宅区绿化越好.
如图,某房产开发商计划在一正方形土地ABCD内建造一个三角形住宅区,在其余土地种植绿化,住宅区形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知,∠PAQ=$\frac{π}{4}$,设∠PAB=θ,记绿化率L=1-$\frac{△PAQ面积}{正方形ABCD面积}$,若L越大,则住宅区绿化越好.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com