
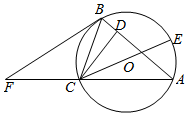
 如图,已知AB=AC,圆O是△ABC的外接圆,CD⊥AB,CE是圆O的直径.过点B作圆O的切线交AC的延长线于点F.
如图,已知AB=AC,圆O是△ABC的外接圆,CD⊥AB,CE是圆O的直径.过点B作圆O的切线交AC的延长线于点F.分析 (Ⅰ)连接AE,证明Rt△CBD∽Rt△CEA,结合AB=AC,即可证明:AB•CB=CD•CE;
(Ⅱ)证明△ABF~△BCF,可得AC=CF,利用切割线定理有FA•FC=FB2,求出AC,即可求△ABC的面积.
解答 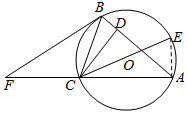 证明:(Ⅰ)连接AE,∵CE是直径,∴∠CAE=90°,
证明:(Ⅰ)连接AE,∵CE是直径,∴∠CAE=90°,
又CD⊥AB,∴∠CDB=90°,
∵∠CBD=∠CEA,故Rt△CBD∽Rt△CEA,…(2分)
∴$\frac{CD}{CB}=\frac{AC}{CE}$,∴AC•CB=CD•CE
又AB=AC,∴AB•CB=CD•CE.…(5分)
(Ⅱ)∵FB是⊙O的切线,∴∠CBF=∠CAB.
∴在△ABF和△BCF中,$\left\{\begin{array}{l}∠FAB=∠FBC\\∠AFB=∠CFB\end{array}\right.$,∴△ABF~△BCF,
∴$\frac{FB}{BC}=\frac{AF}{AB}=\frac{{2\sqrt{2}}}{{\sqrt{2}}}=2$,∴FA=2AB=2AC,∴AC=CF…(7分)
设AC=x,则根据切割线定理有FA•FC=FB2
∴x•2x=8,∴x=2,
∴${S_{△ABC}}=\frac{1}{2}×\sqrt{2}×\sqrt{4-\frac{1}{2}}=\frac{{\sqrt{7}}}{2}$.…(10分)
点评 本题主要考查了切线的性质及其应用,同时考查了相似三角形的判定和切割线定理等知识点,属于中档题.


科目:高中数学 来源: 题型:解答题
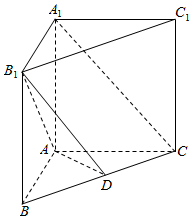 如图,直三棱柱ABC-A1B1C1中,AB=AC=2,AA1=3,D为BC中点,
如图,直三棱柱ABC-A1B1C1中,AB=AC=2,AA1=3,D为BC中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
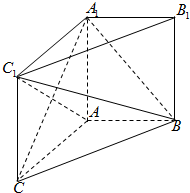 如图,在直三棱柱ABC-A1B1C1中,AC=AA1=4,AB=3,AB⊥AC.
如图,在直三棱柱ABC-A1B1C1中,AC=AA1=4,AB=3,AB⊥AC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 14 | B. | $\frac{{21\sqrt{3}}}{2}$ | C. | 22 | D. | $\frac{{27\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图①,在△ABC中,已知AB=15,BC=14,CA=13.将△ABC沿BC边上的高AD折成一个如图②所示的四面体A-BCD,使得图②中的BC=11.
如图①,在△ABC中,已知AB=15,BC=14,CA=13.将△ABC沿BC边上的高AD折成一个如图②所示的四面体A-BCD,使得图②中的BC=11.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
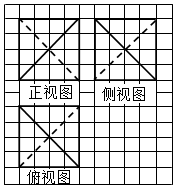
| A. | $\frac{64}{3}$ | B. | $\frac{32}{3}$ | C. | $\frac{64}{3}$或32 | D. | $\frac{32}{3}$或$\frac{64}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com