
分析 利用圆的参数方程,结合配方法,即可求出4(x-$\frac{1}{2}$)2+(y-1)2+4xy的最大值.
解答 解:由题意,设x=2cosα,y=2sinα,
则t=2x+y=4cosα+2sinα=2$\sqrt{5}$sin(α+θ)∈[-2$\sqrt{5}$,2$\sqrt{5}$].
4(x-$\frac{1}{2}$)2+(y-1)2+4xy=4x2+4xy+y2-4x-2y+2=(2x+y)2-2(2x+y)+2=(t-1)2+1
∴t=-2$\sqrt{5}$时,4(x-$\frac{1}{2}$)2+(y-1)2+4xy的最大值是22+4$\sqrt{5}$.
故答案为:22+4$\sqrt{5}$.
点评 本题考查4(x-$\frac{1}{2}$)2+(y-1)2+4xy的最大值,考查圆的参数方程,考查配方法的运用,正确变形是关键.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源: 题型:选择题
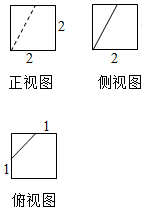 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{47}{6}$ | B. | $\frac{15}{2}$ | C. | $\frac{23}{3}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
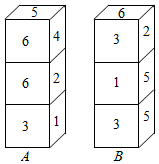 将数字1,2,3,4,5,6书写在每一个骰子的六个表面上,做成6枚一样的骰子.分别取三枚同样的这种骰子叠放成如图A和B所示的两个柱体,则柱体A和B的表面(不含地面)数字之和分别是( )
将数字1,2,3,4,5,6书写在每一个骰子的六个表面上,做成6枚一样的骰子.分别取三枚同样的这种骰子叠放成如图A和B所示的两个柱体,则柱体A和B的表面(不含地面)数字之和分别是( )| A. | 47,48 | B. | 47,49 | C. | 49,50 | D. | 50,49 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
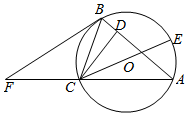 如图,已知AB=AC,圆O是△ABC的外接圆,CD⊥AB,CE是圆O的直径.过点B作圆O的切线交AC的延长线于点F.
如图,已知AB=AC,圆O是△ABC的外接圆,CD⊥AB,CE是圆O的直径.过点B作圆O的切线交AC的延长线于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com