
分析 (1)构造辅助函数ϕ(x)=f(x)-f(x0)-f'(x0)(x-x0),求导,根据函数的单调性求得ϕ(x)的极大值,ϕ(x)≤ϕ(x0)=0,即可得f(x)≤f(x0)+f'(x0)(x-x0);
(2)由(1)可知,两边分别同乘以λ1,λ2,λ3,…λn,采用累加法,得λ1f(x1)+λ2f(x2)+…+λnf(xn)≤(λ1+λ2+…+λn)f(x0)+f'(x0)•[λ1(x1-x0)+λ2(x2-x0)+…+λn(xn-x0)],由λ1+λ2+…+λn=1,设x0=λ1x1+λ2x2+…+λnxn,则λ1(x1-x0)+λ2(x2-x0)+…+λn(xn-x0)=0,即可证明
λ1f(x1)+λ2f(x2)+…+λnf(xn)≤f(λ1x1+λ2x2+…+λnxn);
(3)分别求得f(a)=aq,f[f(a)]=aq2,f{f[f[f(a}}=aq3,λx1+(1-λ)x2=aq,f[λx1+(1-λ)x2]=f(aq)=f[f(a)]=aq2,可得:$λf({x_1})+(1-λ)f({x_2})=a{q^2}$=f[λx1+(1-λ)x2],由n=2,λ1=λ,λ2=1-λ,即λf(x1)+(1-λ)f(x2)≤f[λx1+(1-λ)x2],当且仅当x1=x2时成立,即a=aq2⇒a=1,可得f(a)=a.
解答 解:(1)证明:设ϕ(x)=f(x)-f(x0)-f'(x0)(x-x0),则ϕ'(x)=f'(x)-f'(x0)
∵g'(x)<0故g(x)=f'(x)为减函数,则x=x0为ϕ(x)的极大值点.
∵ϕ(x)≤ϕ(x0)=0,即f(x)≤f(x0)+f'(x0)(x-x0)(当且仅当在x=x0取到)
(2)证明:由(1)可知:f(x1)≤f(x0)+f'(x0)(x1-x0),
两边同乘以λ1得λ1f(x1)≤λ1f(x0)+λ1f'(x0)(x1-x0),
λ2f(x2)≤λ2f(x0)+λ2f'(x0)(x2-x0),
…
λnf(xn)≤λnf(x0)+λnf'(x0)(xn-x0),
上式各式相加,得λ1f(x1)+λ2f(x2)+…+λnf(xn)≤(λ1+λ2+…+λn)f(x0)+f'(x0)•[λ1(x1-x0)+λ2(x2-x0)+…+λn(xn-x0)],
因为λ1+λ2+…+λn=1,设x0=λ1x1+λ2x2+…+λnxn,则λ1(x1-x0)+λ2(x2-x0)+…+λn(xn-x0)=0,
由此,λ1f(x1)+λ2f(x2)+…+λnf(xn)≤f(λ1x1+λ2x2+…+λnxn))
等号当且仅当在x1=x2=…=xn时成立,
(3)证明:记公比为q,q>0,则f(a)=aq,f[f(a)]=aq2,f{f[f[f(a}}=aq3,
取x1′=a,${x_2}=a{q^2}$,λ=$\frac{q}{1+q}$∈(0,1),
则λx1+(1-λ)x2=aq,f[λx1+(1-λ)x2]=f(aq)=f[f(a)]=aq2,
又∵λf(x1)+(1-λ)f(x2)=λf(a)+(1-λ)f(aq2),
=λf(a)+(1-λ)f{f[f(a)]},
=λaq+(1-λ)aq3,
=aq3+λaq-λaq3,
=aq3+λaq(1-q2),
=aq3+$\frac{q}{1+q}$aq(1-q2),
=aq2,
即aq3+$\frac{q}{1+q}$λaq(1-q2)=aq2=f[λx1+(1-λ)x2],
在(2)中取n=2,λ1=λ,λ2=1-λ,即λf(x1)+(1-λ)f(x2)≤f[λx1+(1-λ)x2],
当且仅当x1=x2时成立,即a=aq2⇒q=1,
∴f(a)=a.
点评 本题考查利用导数证明不等式恒成立,等比数列通项公式,考查“累加法“和“构造法”,考查分析问题及解决问题得能力,属于难题.


科目:高中数学 来源: 题型:解答题
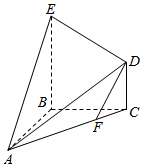 如图,在几何体ABCDE中,BE⊥平面ABC,CD∥BE,△ABC是等腰直角三角形,∠ABC=90°,且BE=AB=4,CD=2,点F在线段AC上,且AF=3FC
如图,在几何体ABCDE中,BE⊥平面ABC,CD∥BE,△ABC是等腰直角三角形,∠ABC=90°,且BE=AB=4,CD=2,点F在线段AC上,且AF=3FC查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图①,在△ABC中,已知AB=15,BC=14,CA=13.将△ABC沿BC边上的高AD折成一个如图②所示的四面体A-BCD,使得图②中的BC=11.
如图①,在△ABC中,已知AB=15,BC=14,CA=13.将△ABC沿BC边上的高AD折成一个如图②所示的四面体A-BCD,使得图②中的BC=11.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
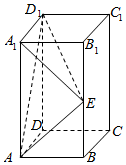 长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.
长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四棱锥P-ABCD,ABCD是菱形,三角形APD是等边三角形,E是PD中点
如图,已知四棱锥P-ABCD,ABCD是菱形,三角形APD是等边三角形,E是PD中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com