
分析 设MN=2MA,利用代入法求出N的轨迹方程,可得ON|min=$\sqrt{64+36}$-2$\sqrt{2}$=10-2$\sqrt{2}$,利用MO+2MA=MO+MN=ON,即可求出MO+2MA的最小值.
解答 解:设MN=2MA,N(x,y),M(a,b),则a=12-x,b=-2-y,
代入圆C:(x-4)2+(y-4)2=8可得(12-x-4)2+(-2-y-4)2=8,
即N的轨迹方程是(x-8)2+(y+6)2=8,
∴|ON|min=$\sqrt{64+36}$-2$\sqrt{2}$=10-2$\sqrt{2}$,
∵MO+2MA=MO+MN=ON,
∴MO+2MA的最小值为10-2$\sqrt{2}$,
故答案为:10-2$\sqrt{2}$.
点评 本题考查MO+2MA的最小值,考查代入法求轨迹方程,考查学生的计算能力,正确转化是关键.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一几何体的三视图如图所示,若将该几何体切割成长方体,则长方体的最大体积与该几何体的体积之比为( )
一几何体的三视图如图所示,若将该几何体切割成长方体,则长方体的最大体积与该几何体的体积之比为( )| A. | $\frac{2}{3}$ | B. | $\frac{36}{41}$ | C. | $\frac{18}{23}$ | D. | $\frac{9}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,OM,ON是两条海岸线,Q为海中一个小岛,A为海岸线OM上的一个码头.已知tan∠MON=-3,OA=6km,Q到海岸线OM,ON的距离分别为3km,$\frac{{6\sqrt{10}}}{5}$km.现要在海岸线ON上再建一个码头,使得在水上旅游直线AB经过小岛Q.
如图,OM,ON是两条海岸线,Q为海中一个小岛,A为海岸线OM上的一个码头.已知tan∠MON=-3,OA=6km,Q到海岸线OM,ON的距离分别为3km,$\frac{{6\sqrt{10}}}{5}$km.现要在海岸线ON上再建一个码头,使得在水上旅游直线AB经过小岛Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
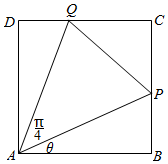 如图,某房产开发商计划在一正方形土地ABCD内建造一个三角形住宅区,在其余土地种植绿化,住宅区形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知,∠PAQ=$\frac{π}{4}$,设∠PAB=θ,记绿化率L=1-$\frac{△PAQ面积}{正方形ABCD面积}$,若L越大,则住宅区绿化越好.
如图,某房产开发商计划在一正方形土地ABCD内建造一个三角形住宅区,在其余土地种植绿化,住宅区形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知,∠PAQ=$\frac{π}{4}$,设∠PAB=θ,记绿化率L=1-$\frac{△PAQ面积}{正方形ABCD面积}$,若L越大,则住宅区绿化越好.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[20,30)内的概率为( )
如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[20,30)内的概率为( )| A. | 0.2 | B. | 0.4 | C. | 0.5 | D. | 0.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com