
 ��ͼ��OM��ON�����������ߣ�QΪ����һ��С����AΪ������OM�ϵ�һ����ͷ����֪tan��MON=-3��OA=6km��Q��������OM��ON�ľ���ֱ�Ϊ3km��$\frac{{6\sqrt{10}}}{5}$km����Ҫ�ں�����ON���ٽ�һ����ͷ��ʹ����ˮ������ֱ��AB����С��Q��
��ͼ��OM��ON�����������ߣ�QΪ����һ��С����AΪ������OM�ϵ�һ����ͷ����֪tan��MON=-3��OA=6km��Q��������OM��ON�ľ���ֱ�Ϊ3km��$\frac{{6\sqrt{10}}}{5}$km����Ҫ�ں�����ON���ٽ�һ����ͷ��ʹ����ˮ������ֱ��AB����С��Q������ ��1���ɵ㵽ֱ�ߵľ��룬���ֱ��AQ�ķ��̣��������AB�ij���
��2��ǿˮ�����Შ�����ֵĺ��м�$P{C^2}��{r^2}��t��[{0��\frac{1}{2}}]�����$��������з������ۣ����ɵó����ۣ�
��� 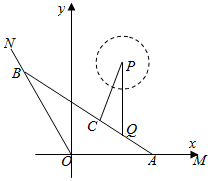 �⣺��1���Ե�O Ϊ����ԭ�㣬ֱ��OM Ϊx �ᣬ����ֱ������ϵ��ͼ��ʾ��
�⣺��1���Ե�O Ϊ����ԭ�㣬ֱ��OM Ϊx �ᣬ����ֱ������ϵ��ͼ��ʾ��
��������ã�A��6��0����ֱ��ON �ķ���Ϊy=-3x��Q��x0��3����x0��0����
��$\frac{{|{3{x_0}+3}|}}{{\sqrt{10}}}=\frac{{6\sqrt{10}}}{5}$����x0��0 ��x0=3����Q��3��3����
��ֱ��AQ �ķ���Ϊy=-��x-6������x+y-6=0��
��$\left\{{\begin{array}{l}{y=-3x}\\{x+y-6=0}\end{array}}\right.$ ��$\left\{{\begin{array}{l}{x=-3}\\{y=9}\end{array}}\right.$ ��B��-3��9����
��$AB=\sqrt{{{��{-3-6}��}^2}+{9^2}}=9\sqrt{2}$��
��ˮ��������AB �ij�Ϊ$9\sqrt{2}km$��
��2�������������ǿˮ��ԲP��
������ɵ�P��3��9��������t Сʱʱ���������߶�AB �ϵĵ�C ������
AC=18$\sqrt{2}$t��0$��t��\frac{1}{2}$����C��6-18t��18t����
ǿˮ�����Შ�����ֵĺ��м�$P{C^2}��{r^2}��t��[{0��\frac{1}{2}}]�����$��
PC2=��18t-3��2+��18t-9��2��r2=9at��
��t=0 ʱ����ʽ�������
��$t��0ʱ����t�ʣ�{0��\frac{1}{2}}]ʱ$��$a��72t+\frac{10}{t}-48$.$��g��t��=72t+\frac{10}{t}-48��t�ʣ�{0��\frac{1}{2}}]$��$g��t��=72t+\frac{10}{t}-48��24\sqrt{5}-48$�����ҽ���$t=\frac{{\sqrt{5}}}{6}�ʣ�0��\frac{1}{2}]$ ʱ�Ⱥų�����
���ԣ���0��a��24$\sqrt{5}$-48 ʱr��PC ��������༴ǿˮ�����Შ�����ֵĺ��У�
���� ���⿼��ֱ����Բ��λ�ù�ϵ�����������е�ʵ��Ӧ�ã�ע��Բ�����ʡ�ֱ�߷��̵ĺ��������ǽ���Ĺؼ��������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
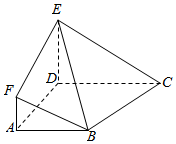 ��ͼ��ʾ��ƽ���ı���ADEF������ABCD���ڵ�ƽ�滥�ഹֱ��AD��CD��AD��ED��AF��DE��AB��CD��CD=2AB=2AD=2ED=xAF��
��ͼ��ʾ��ƽ���ı���ADEF������ABCD���ڵ�ƽ�滥�ഹֱ��AD��CD��AD��ED��AF��DE��AB��CD��CD=2AB=2AD=2ED=xAF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
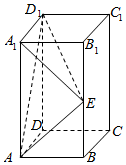 ������ABCD-A1B1C1D1�У�AB=BC=1��AA1=2��E�Dz���BB1���е㣮
������ABCD-A1B1C1D1�У�AB=BC=1��AA1=2��E�Dz���BB1���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2��b2 | B�� | ab��b2 | C�� | a-b��0 | D�� | |a|+|b|=|a+b| |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ֱ�� | B�� | һ��ֱ�� | ||
| C�� | һ���� | D�� | һ�����һ��ֱ�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com