
分析 (1)得到-3,-2是方程$\frac{2x}{{x}^{2}+6}$-k=0的根,将x=-2或-3代入方程求出k的值即可;
(2)根据函数的单调性求出f(x)的最小值,从而求出k的范围即可.
解答 解:(1)f(x)=$\frac{2x}{{x}^{2}+6}$,若f(x)>k的解集为{x|x<-3或x>-2},
则-3,-2是方程$\frac{2x}{{x}^{2}+6}$-k=0的根,
解得:k=-$\frac{2}{5}$;
(2)若对任意x<0,f(x)≥t恒成立,
即若对任意x<0,f(x)min≥t,f′(x)=$\frac{-{2x}^{2}+12}{{{(x}^{2}+6)}^{2}}$,
令f′(x)>0,解得:-$\sqrt{6}$<x<0,
令f′(x)<0,解得:x<-$\sqrt{6}$,
故f(x)在(-∞,-$\sqrt{6}$)递减,在(-$\sqrt{6}$,0)递增,
∴f(x)min=f(-$\sqrt{6}$)=-$\frac{\sqrt{6}}{6}$,
∴t≤-$\frac{\sqrt{6}}{6}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式问题,是一道中档题.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:选择题
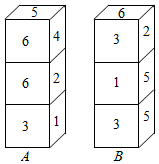 将数字1,2,3,4,5,6书写在每一个骰子的六个表面上,做成6枚一样的骰子.分别取三枚同样的这种骰子叠放成如图A和B所示的两个柱体,则柱体A和B的表面(不含地面)数字之和分别是( )
将数字1,2,3,4,5,6书写在每一个骰子的六个表面上,做成6枚一样的骰子.分别取三枚同样的这种骰子叠放成如图A和B所示的两个柱体,则柱体A和B的表面(不含地面)数字之和分别是( )| A. | 47,48 | B. | 47,49 | C. | 49,50 | D. | 50,49 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,OM,ON是两条海岸线,Q为海中一个小岛,A为海岸线OM上的一个码头.已知tan∠MON=-3,OA=6km,Q到海岸线OM,ON的距离分别为3km,$\frac{{6\sqrt{10}}}{5}$km.现要在海岸线ON上再建一个码头,使得在水上旅游直线AB经过小岛Q.
如图,OM,ON是两条海岸线,Q为海中一个小岛,A为海岸线OM上的一个码头.已知tan∠MON=-3,OA=6km,Q到海岸线OM,ON的距离分别为3km,$\frac{{6\sqrt{10}}}{5}$km.现要在海岸线ON上再建一个码头,使得在水上旅游直线AB经过小岛Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
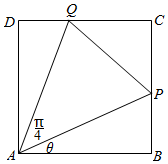 如图,某房产开发商计划在一正方形土地ABCD内建造一个三角形住宅区,在其余土地种植绿化,住宅区形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知,∠PAQ=$\frac{π}{4}$,设∠PAB=θ,记绿化率L=1-$\frac{△PAQ面积}{正方形ABCD面积}$,若L越大,则住宅区绿化越好.
如图,某房产开发商计划在一正方形土地ABCD内建造一个三角形住宅区,在其余土地种植绿化,住宅区形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知,∠PAQ=$\frac{π}{4}$,设∠PAB=θ,记绿化率L=1-$\frac{△PAQ面积}{正方形ABCD面积}$,若L越大,则住宅区绿化越好.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 我国是世界上严重缺水的国家.某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨).将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家.某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨).将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com