
分析 (1)设出动点的坐标,利用向量条件确定动点坐标之间的关系,利用M为圆C上任意一点,即可求得结论;
(2)由(1)可得两个圆的圆心在直线y=x上,|$\overrightarrow{AM}$+$\overrightarrow{AN}$|的最大值为|OC|+2-1,即可求出求|$\overrightarrow{AM}$+$\overrightarrow{AN}$|的最大值.
解答 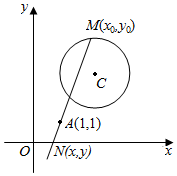 解:(1)设N(x,y),M(x0,y0),则
解:(1)设N(x,y),M(x0,y0),则
由$\overrightarrow{MA}$=2$\overrightarrow{AN}$得(1-x0,1-y0)=2(x-1,y-1),
∴1-x0=2x-2,1-y0=2y-2,即x0=3-2x,y0=3-2y,
∵M为圆C上任意一点
∴(x0-3)2+(y0-3)2=4,
∴(3-2x-3)2+(3-2y-3)2=4,
∴x2+y2=1.
即点N的轨迹方程是x2+y2=1;
(2)由(1)可得两个圆的圆心在直线y=x上,
∴|$\overrightarrow{AM}$+$\overrightarrow{AN}$|的最大值为|OC|+2-1=$\sqrt{9+9}$+1=3$\sqrt{2}$+1.
点评 本题考查轨迹方程,解题的关键是利用向量条件确定动点坐标之间的关系,属于中档题.


科目:高中数学 来源: 题型:解答题
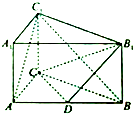 如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AB=5,BC=4,AC=CC1=3,D为AB的中点
如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AB=5,BC=4,AC=CC1=3,D为AB的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,OM,ON是两条海岸线,Q为海中一个小岛,A为海岸线OM上的一个码头.已知tan∠MON=-3,OA=6km,Q到海岸线OM,ON的距离分别为3km,$\frac{{6\sqrt{10}}}{5}$km.现要在海岸线ON上再建一个码头,使得在水上旅游直线AB经过小岛Q.
如图,OM,ON是两条海岸线,Q为海中一个小岛,A为海岸线OM上的一个码头.已知tan∠MON=-3,OA=6km,Q到海岸线OM,ON的距离分别为3km,$\frac{{6\sqrt{10}}}{5}$km.现要在海岸线ON上再建一个码头,使得在水上旅游直线AB经过小岛Q.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤0} | B. | {x|2≤x≤4} | C. | {x|0<x≤2或x≥4} | D. | {x|0≤x<2或x>4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com