
分析 (Ⅰ)先求出函数的定义域,求出函数f(x)的导函数,由已知函数f(x)=x2-alnx在x=1处取得极值,即f'(1)=0,求出a的值,然后检验,满足题意即可;
(Ⅱ)由(Ⅰ)得$f'(x)=2x-\frac{a}{x}=\frac{{2{x^2}-a}}{x}$,定义域为(0,+∞),然后分类讨论,当a≤0时,f(x)的单调增区间为[1,+∞),最小值为f(1)=1;当0<a≤2,f(x)在区间[1,+∞)上单调递增,最小值为f(1)=1;当a>2时,函数f(x)在$x=\sqrt{\frac{a}{2}}$取得最小值$\frac{a}{2}-\frac{a}{2}ln\frac{a}{2}$,综上当a≤2时,f(x)在区间[1,+∞)上的最小值为1;当a>2时,f(x)在区间[1,+∞)上的最小值为$\frac{a}{2}-\frac{a}{2}ln\frac{a}{2}$;
(Ⅱ)由h(x)=x2-f(x)得h(x)=2lnx,当1<x<e2时,0<lnx<2,0<h(x)<4,欲证$x<\frac{4+h(x)}{4-h(x)}$,只需证x[4-h(x)]<4+h(x),即$lnx>\frac{2x-2}{x+1}$,设$φ(x)=lnx-\frac{2x-2}{x+1}$,求出φ'(x),当1<x<e2时,φ'(x)>0,φ(x)在区间(1,e2)上单调递增,当1<x<e2时,φ(x)>φ(1)=0,即$lnx-\frac{2x-2}{x+1}>0$,则可证明结论成立.
解答 (Ⅰ)解:由f(x)=x2-alnx,定义域为(0,+∞),
得$f'(x)=2x-\frac{a}{x}$.
∵函数f(x)=x2-alnx在x=1处取得极值,
∴f'(1)=0,即2-a=0,解得a=2.
经检验,满足题意,∴a=2;
(Ⅱ)解:由(Ⅰ)得$f'(x)=2x-\frac{a}{x}=\frac{{2{x^2}-a}}{x}$,定义域为(0,+∞).
当a≤0时,有f'(x)>0,f(x)在区间[1,+∞)上单调递增,最小值为f(1)=1;
当0<a≤2,由f'(x)=0得$x=\sqrt{\frac{a}{2}}$,且$0<\sqrt{\frac{a}{2}}≤1$.
当$x∈(0,\sqrt{\frac{a}{2}})$时,f'(x)<0,f(x)单调递减,当$x∈(\sqrt{\frac{a}{2}}\;,\;+∞)$时,f'(x)>0,f(x)单调递增,
∴f(x)在区间[1,+∞)上单调递增,最小值为f(1)=1;
当a>2时,$\sqrt{\frac{a}{2}}>1$,
当$x∈(1,\sqrt{\frac{a}{2}})$时,f'(x)<0,f(x)单调递减,当$x∈(\sqrt{\frac{a}{2}}\;,\;+∞)$时,f'(x)>0,f(x)单调递增,
∴函数f(x)在$x=\sqrt{\frac{a}{2}}$取得最小值$f(\sqrt{\frac{a}{2}})=\frac{a}{2}-\frac{a}{2}ln\frac{a}{2}$.
综上当a≤2时,f(x)在区间[1,+∞)上的最小值为1;
当a>2时,f(x)在区间[1,+∞)上的最小值为$\frac{a}{2}-\frac{a}{2}ln\frac{a}{2}$.
(Ⅲ)证明:由h(x)=x2-f(x)得h(x)=2lnx.
当1<x<e2时,0<lnx<2,0<h(x)<4,
欲证$x<\frac{4+h(x)}{4-h(x)}$,只需证x[4-h(x)]<4+h(x),
即证$h(x)>\frac{4x-4}{x+1}$,即$lnx>\frac{2x-2}{x+1}$.
设$φ(x)=lnx-\frac{2x-2}{x+1}$,
则$φ'(x)=\frac{1}{x}-\frac{2(x+1)-(2x-2)}{{{{(x+1)}^2}}}=\frac{{{{(x-1)}^2}}}{{x{{(x+1)}^2}}}$.
当1<x<e2时,φ'(x)>0,∴φ(x)在区间(1,e2)上单调递增.
∴当1<x<e2时,φ(x)>φ(1)=0,即$lnx-\frac{2x-2}{x+1}>0$,
故$x<\frac{4+h(x)}{4-h(x)}$.
∴当1<x<e2时,$x<\frac{4+h(x)}{4-h(x)}$恒成立.
点评 本题考查了利用导数研究函数的单调性,考查了利用导数研究函数的极值问题,考查了学生的运算能力,计算量比较大,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
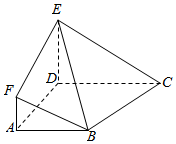 如图所示,平面四边形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AD⊥ED,AF∥DE,AB∥CD,CD=2AB=2AD=2ED=xAF.
如图所示,平面四边形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AD⊥ED,AF∥DE,AB∥CD,CD=2AB=2AD=2ED=xAF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
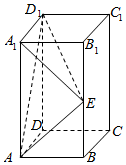 长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.
长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2>b2 | B. | ab>b2 | C. | a-b<0 | D. | |a|+|b|=|a+b| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com