
 如图,已知四棱锥P-ABCD,ABCD是菱形,三角形APD是等边三角形,E是PD中点
如图,已知四棱锥P-ABCD,ABCD是菱形,三角形APD是等边三角形,E是PD中点分析 (1)连接BD交AC于O,则O为BD中点,故而OE∥PB,于是PB∥平面ACE;
(2)由AC⊥BD,AC⊥PB得出AC⊥平面PBD,故而AC⊥PD,结合AE⊥PD得出PD⊥平面ACE,故而平面ACE⊥平面PAD.
解答 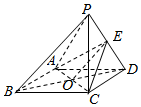 解:(1)PB∥平面ACE.
解:(1)PB∥平面ACE.
证明:连接BD交AC于O,连接OE,
∵四边形ABCD是菱形,
∴O是BD的中点,又E是PD的中点,
∴OE∥PB.又OE?平面ACE,PB?平面ACE,
∴PB∥平面ACE.
(2)∵四边形ABCD的菱形,
∴AC⊥BD.
又AC⊥PB,PB?平面PBD,BD?平面PBD,PB∩BD=B,
∴AC⊥平面PBD,又PD?平面PBD,
∴AC⊥PD.
∵△APD是等边三角形,E是PD中点,
AE⊥PD.
又AC?平面ACE,AE?平面ACE,AC∩AE=A,
∴PD⊥平面ACE,又PD?平面PAD,
∴平面PAD⊥平面ACE.
点评 本题考查了线面平行,面面垂直的判定,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
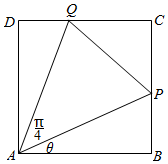 如图,某房产开发商计划在一正方形土地ABCD内建造一个三角形住宅区,在其余土地种植绿化,住宅区形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知,∠PAQ=$\frac{π}{4}$,设∠PAB=θ,记绿化率L=1-$\frac{△PAQ面积}{正方形ABCD面积}$,若L越大,则住宅区绿化越好.
如图,某房产开发商计划在一正方形土地ABCD内建造一个三角形住宅区,在其余土地种植绿化,住宅区形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知,∠PAQ=$\frac{π}{4}$,设∠PAB=θ,记绿化率L=1-$\frac{△PAQ面积}{正方形ABCD面积}$,若L越大,则住宅区绿化越好.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 我国是世界上严重缺水的国家.某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨).将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家.某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨).将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[20,30)内的概率为( )
如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[20,30)内的概率为( )| A. | 0.2 | B. | 0.4 | C. | 0.5 | D. | 0.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com