
 ��ͼ�٣��ڡ�ABC�У���֪AB=15��BC=14��CA=13������ABC��BC���ϵĸ�AD�۳�һ����ͼ����ʾ��������A-BCD��ʹ��ͼ���е�BC=11��
��ͼ�٣��ڡ�ABC�У���֪AB=15��BC=14��CA=13������ABC��BC���ϵĸ�AD�۳�һ����ͼ����ʾ��������A-BCD��ʹ��ͼ���е�BC=11������ ��1������ͼ����֮ǰ����֮��ı߳���ϵ����϶���ǵĶ��������⣮
��2��������������A-BCD����AD�ϴ��ڵ�P��ʹ��$\overrightarrow{PB}•\overrightarrow{PC}=0$���������������Ķ��������������㷨����л�����⣮
��� �⣺��1������֪AD��BD��AD��CD��
�ʶ����B-AD-C��ƽ���Ϊ��BDC��
��ͼ�٣���BD=x��AD=h����CD=14-x��
�ڡ�ABD���ACD�У��ֱ��ù��ɶ�����x2+h2=152����14-x��2+h2=132��
��x=9��h=12���Ӷ�AD=12��BD=9��CD=5��
��ͼ�ڵġ�BCD�У������Ҷ�����BC2=BD2+CD2-2BD•CDcos��BDC��
��112=92+52-2��9��5cos��BDC����cos��BDC=-$\frac{1}{6}$��
�������B-AD-C��ƽ��ǵ�����ֵ��-$\frac{1}{6}$��
��2��������������A-BCD����AD�ϴ��ڵ�P��ʹ��$\overrightarrow{PB}•\overrightarrow{PC}=0$��
��0=$\overrightarrow{PB}•\overrightarrow{PC}$=��$\overrightarrow{PD}$+$\overrightarrow{DB}$��•��$\overrightarrow{PD}$+$\overrightarrow{DC}$��=$\overrightarrow{PD}$2+$\overrightarrow{DB}$•$\overrightarrow{PD}$+$\overrightarrow{PD}$•$\overrightarrow{DC}$+$\overrightarrow{DB}$•$\overrightarrow{DC}$=$\overrightarrow{PD}$2+0+0+9��5����-$\frac{1}{6}$��=$\overrightarrow{PD}$2-$\frac{15}{2}$��
��|$\overrightarrow{PD}$|=$\frac{\sqrt{30}}{2}$��12���������⣬
������AD�ϴ��ڵ�P��ʹ��$\overrightarrow{PB}•\overrightarrow{PC}=0$����ʱ|$\overrightarrow{PD}$|=$\frac{\sqrt{30}}{2}$��
���� ������Ҫ�������ǵļ����Լ�������������Ӧ�ã�����ѧ�������������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
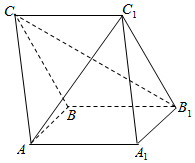 ��ͼ��ʾ����������ABC-A1B1C1�У�AA1B1BΪ�����Σ�BB1C1CΪ���Σ���BB1C1=60�㣬ƽ��AA1B1B��ƽ��BB1C1C��
��ͼ��ʾ����������ABC-A1B1C1�У�AA1B1BΪ�����Σ�BB1C1CΪ���Σ���BB1C1=60�㣬ƽ��AA1B1B��ƽ��BB1C1C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
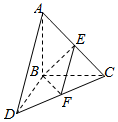 ��ͼ������A-BCD�У���ABC�͡�BCD����ƽ�滥�ഹֱ����BC=BD=4��AC=4$\sqrt{2}$��CD=4$\sqrt{3}����ACB={45��}$��E��F�ֱ�ΪAC��DC���е㣮
��ͼ������A-BCD�У���ABC�͡�BCD����ƽ�滥�ഹֱ����BC=BD=4��AC=4$\sqrt{2}$��CD=4$\sqrt{3}����ACB={45��}$��E��F�ֱ�ΪAC��DC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
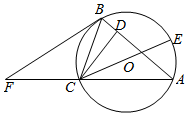 ��ͼ����֪AB=AC��ԲO�ǡ�ABC�����Բ��CD��AB��CE��ԲO��ֱ��������B��ԲO�����߽�AC���ӳ����ڵ�F��
��ͼ����֪AB=AC��ԲO�ǡ�ABC�����Բ��CD��AB��CE��ԲO��ֱ��������B��ԲO�����߽�AC���ӳ����ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 81�� | B�� | 125�� | C�� | ��41+7$\sqrt{145}$���� | D�� | ��73+7$\sqrt{145}$���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
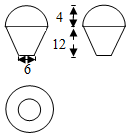
 һ�����������ͼ��ͼ��ʾ�������ü������и�ɳ����壬�������������ü���������֮��Ϊ��������
һ�����������ͼ��ͼ��ʾ�������ü������и�ɳ����壬�������������ü���������֮��Ϊ��������| A�� | $\frac{2}{3}$ | B�� | $\frac{36}{41}$ | C�� | $\frac{18}{23}$ | D�� | $\frac{9}{11}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | -1 | B�� | 0 | C�� | 1 | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com