
已知数列 是等差数列,其前n项和为Sn,若
是等差数列,其前n项和为Sn,若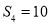 ,
,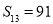 .
.
(1)求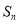 ;
;
(2)若数列{Mn}满足条件:  ,当
,当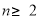 时,
时,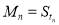 -
-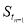 ,其中数列
,其中数列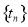 单调递增,且
单调递增,且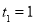 ,
,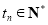 .
.
①试找出一组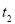 ,
,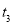 ,使得
,使得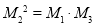 ;
;
②证明:对于数列 ,一定存在数列
,一定存在数列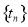 ,使得数列
,使得数列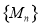 中的各数均为一个整数的平方.
中的各数均为一个整数的平方.
(1)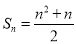 (2)①
(2)①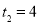 ,
,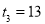 ②详见解析
②详见解析
【解析】
试题分析:(1)求等差数列前n项和,一般利用待定系数法,即确定首项及公差,再代入公式即可:由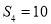 ,
,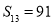 ,得
,得 解得
解得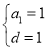 ,所以
,所以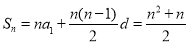 (2)①题目要求找出一组,因此方法为逐一代入验证,若
(2)①题目要求找出一组,因此方法为逐一代入验证,若 由
由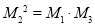 得
得 ,则
,则 无整数解;若
无整数解;若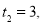 由
由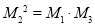 得
得 ,则
,则 无整数解;若
无整数解;若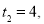 解得
解得 ②从①可归纳
②从①可归纳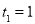 ,
,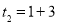 ,
,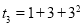 ,则
,则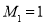 ,
,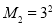 ,
,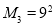 ,一般的取
,一般的取 ,下面只需验证
,下面只需验证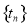 使得数列
使得数列 中的各数均为一个整数的平方.由
中的各数均为一个整数的平方.由 得
得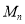 =
=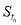 -
-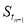 =
=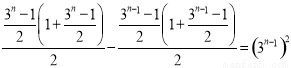 ,为一整数平方.
,为一整数平方.
试题解析:(1)设数列 的首项为
的首项为 ,公差为
,公差为 ,
,
由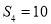 ,
,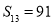 ,得
,得 , 2分
, 2分
解得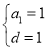 ,
,
所以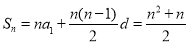 4分
4分
(2)①因为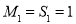 ,
,
若
 ,
, ,
,
因为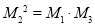 ,
,
所以 ,
, ,此方程无整数解; 6分
,此方程无整数解; 6分
若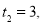
 ,
,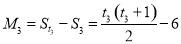 ,
,
因为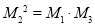 ,
,
所以 ,
, ,此方程无整数解; 8分
,此方程无整数解; 8分
若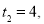
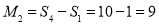 ,
, ,
,
因为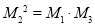 ,
,
所以 ,
,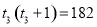 ,解得
,解得 ,
,
所以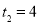 ,
,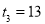 满足题意 10分
满足题意 10分
②由①知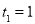 ,
,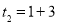 ,
,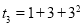 ,则
,则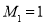 ,
,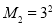 ,
,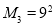 ,
,
一般的取 , 13分
, 13分
此时 ,
, ,
,
则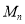 =
=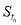 -
-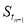 =
=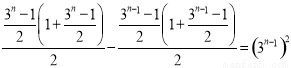 ,
,
所以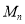 为一整数平方.
为一整数平方.
因此存在数列 ,使得数列
,使得数列 中的各数均为一个整数的平方. 16分
中的各数均为一个整数的平方. 16分
考点:等差数列与等比数列


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源:2014-2015学年北京市东城区示范校高三上学期综合能力测试文科数学试卷(解析版) 题型:解答题
(本小题共13分)设数列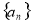 的前
的前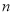 项和为
项和为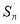 ,且
,且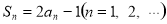 .
.
(1)求数列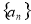 的通项公式;
的通项公式;
(2)若数列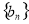 满足
满足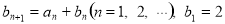 ,求数列
,求数列 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市大兴区高三上学期期末考试文科数学试卷(解析版) 题型:填空题
定义在 上的奇函数
上的奇函数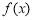 满足
满足 ,且在
,且在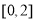 上
上
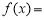
 ,则
,则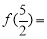 ;若方程
;若方程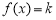 在
在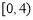 上恰有4个根,则实数
上恰有4个根,则实数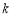 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省泰安市高三上学期期末考试理科数学试卷(解析版) 题型:选择题
已知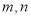 为不同的直线,
为不同的直线,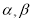 为不同的平面,则下列说法正确的是
为不同的平面,则下列说法正确的是
A.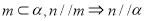
B.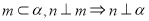
C.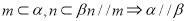
D.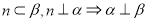
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省宿迁市高三上学期第一次摸底考试文科数学试卷(解析版) 题型:解答题
已知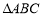 的内角
的内角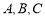 的对边分别为
的对边分别为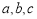 ,
,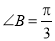 .
.
(1)若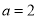 ,
,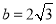 ,求
,求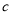 的值;
的值;
(2)若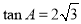 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省宿迁市高三上学期第一次摸底考试理科数学试卷(解析版) 题型:解答题
已知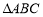 的内角
的内角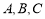 的对边分别为
的对边分别为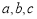 ,
,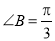 .
.
(1)若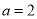 ,
,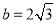 ,求
,求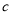 的值;
的值;
(2)若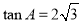 ,求
,求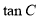 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北唐山市高三上学期期末考试理科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-1:几何证明选讲
如图,四边形ABDC内接于圆,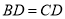 ,过C点的圆的切线与AB的延长线交于E点.
,过C点的圆的切线与AB的延长线交于E点.

(1)求证: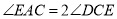 ;
;
(2)若 ,
,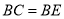 ,
, ,求AB的长.
,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com