
【题目】如图,三棱柱![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.

(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)在给出的坐标系中,画出关于x、y两个相关变量的散点图.
(2)请根据上表提供的数据,用最小二乘法求出变量![]() 关于变量
关于变量![]() 的线性回归直线方程
的线性回归直线方程![]() .
.
(3)预测饲养满12个月时,这种鱼的平均体重(单位:千克).
(参考公式: 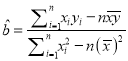 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,(1)求
为奇函数,(1)求![]() 的值;(2)判断并证明函数
的值;(2)判断并证明函数![]() 的单调性;(3)是否存在这样的实数
的单调性;(3)是否存在这样的实数![]() ,使
,使![]() 对一切
对一切![]() 恒成立,若存在,试求出
恒成立,若存在,试求出![]() 取值的集合;若不存在,说明理由.
取值的集合;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位: ![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近8年的年宣传费
(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.


(1)根据散点图判断, ![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型?(给出判断即可,不必说出理由);
的回归方程类型?(给出判断即可,不必说出理由);
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知这种产品的年利润![]() 与
与![]() 的关系为
的关系为![]() ,根据(2)的结果求:年宣传费
,根据(2)的结果求:年宣传费![]() 为何值时,年利润最大?
为何值时,年利润最大?
附:对于一组数据![]() ,
, ![]() ,…
,…![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某港口![]() 要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口
要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口![]() 北偏西
北偏西![]() 且与该港口相距20海里的
且与该港口相距20海里的![]() 处,并以30海里/时的航行速度沿正东方向匀速行驶,假设该小船沿直线方向以
处,并以30海里/时的航行速度沿正东方向匀速行驶,假设该小船沿直线方向以![]() 海里/时的航行速度匀速行驶,经过
海里/时的航行速度匀速行驶,经过![]() 小时与轮船相遇.
小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)假设小艇的最高航行速度只能达到30海里/时,试设计航行方案(即确定航行方向与航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D中,M为DD1的中点,O为AC的中点,AB=2.

(I)求证:BD1∥平面ACM;
(Ⅱ)求证:B1O⊥平面ACM;
(Ⅲ)求三棱锥O-AB1M的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测验中,有6位同学的平均成绩为75分, 用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
编号n | 1 | 2 | 3 | 4 | 5 |
成绩xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com