
【题目】在正方体ABCD-A1B1C1D中,M为DD1的中点,O为AC的中点,AB=2.

(I)求证:BD1∥平面ACM;
(Ⅱ)求证:B1O⊥平面ACM;
(Ⅲ)求三棱锥O-AB1M的体积.
【答案】(Ⅰ)(Ⅱ)详见解析;(Ⅲ)![]() .
.
【解析】
试题分析:(Ⅰ)要证明线面平行,可先证明线线平行,连接BD,MO,根据三角形中位线的平行关系可证明![]() ;(Ⅱ)要证明线面垂直,根据判定定理,可证明线与平面内的两条相交直线垂直,即证明
;(Ⅱ)要证明线面垂直,根据判定定理,可证明线与平面内的两条相交直线垂直,即证明![]() 和
和![]() ;(Ⅲ)将四面体的体积转化为以三角形
;(Ⅲ)将四面体的体积转化为以三角形![]() 当底面,AO是四面体的高的几何体的体积,这样易计算四面体的体积.
当底面,AO是四面体的高的几何体的体积,这样易计算四面体的体积.
试题解析:(I)证明:
连结BD,设BD与AC的交点为O,
∵AC,BD为正方形的对角线,故O为BD中点;
连结MO,
∵O,M分别为DB,DD1的中点,
∴OM∥BD1,…(2分)
∵OM平面ACM,BD1平面ACM…(3分)
∴BD1∥平面ACM. …(4分)
(II)∵AC⊥BD,DD1⊥平面ABCD,且AC平面ABCD,
∴AC⊥DD1;且BD∩DD1=D,∴AC⊥平面BDD1B1…(6分)
OB1平面BDD1B1,∴B1O⊥AC,…(7分)
连结B1M,在△B1MO中 ![]()
∴![]()
∴B1O⊥OM…(10分)
又OM∩AC=O,∴B1O⊥平面AMC; …(11分)
.(II) V=![]()



科目:高中数学 来源: 题型:
【题目】某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是![]() ,样本数据分组为
,样本数据分组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直方图中![]() 的值;
的值;
(2)如果上学路上所需时间不少于60分钟的学生可申请在学校住宿,请估计学校1000名新生中有多少名学生可以申请住宿;
(3)现有6名上学路上时间小于![]() 分钟的新生,其中2人上学路上时间小于
分钟的新生,其中2人上学路上时间小于![]() 分钟. 从这6人中任选2人,设这2人中上学路上时间小于
分钟. 从这6人中任选2人,设这2人中上学路上时间小于![]() 分钟人数为
分钟人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用![]() 表示学生掌握和接受概念的能力(
表示学生掌握和接受概念的能力(![]() 的值越大,表示接受能力越强),
的值越大,表示接受能力越强),![]() 表示提出和讲授概念的时间(单位:分),可以有以下公式:
表示提出和讲授概念的时间(单位:分),可以有以下公式: 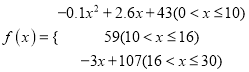 .
.
(1)开讲多少分钟后,学生的接受能力最强?能维持多少分钟?
(2)开讲5分钟与开讲20分钟比较,学生的接受能力何时强一些?
(3)一个数学难题,需要55的接受能力以及13分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 是正三角形,且与底面
是正三角形,且与底面![]() 垂直,底面
垂直,底面![]() 是边长为2的菱形,
是边长为2的菱形, ![]() 是
是![]() 的中点,过
的中点,过![]() 三点的平面交
三点的平面交![]() 于
于![]() ,
, ![]() 为
为![]() 的中点,求证:
的中点,求证:

(1)![]() 平面
平面![]() ;
;
(2)![]() 平面
平面![]() ;
;
(3)平面![]() 平面
平面![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com