
分析 用$\overrightarrow{CP},\overrightarrow{CQ}$表示出$\overrightarrow{CG}$,根据P,G,Q三点共线列出方程得出m,n的关系.
解答 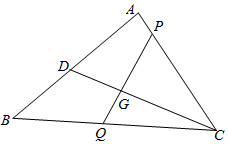 解取AB中点D,连结CD,则$\overrightarrow{CD}=\frac{1}{2}\overrightarrow{CA}+\frac{1}{2}\overrightarrow{CB}$,
解取AB中点D,连结CD,则$\overrightarrow{CD}=\frac{1}{2}\overrightarrow{CA}+\frac{1}{2}\overrightarrow{CB}$,
∵G是△ABC的重心,∴$\overrightarrow{CG}=\frac{2}{3}$$\overrightarrow{CD}$=$\frac{1}{3}$$\overrightarrow{CA}$+$\frac{1}{3}$$\overrightarrow{CB}$.
∵$\overrightarrow{CP}$=m$\overrightarrow{CA}$,$\overrightarrow{CQ}$=n$\overrightarrow{CB}$,
∴$\overrightarrow{CA}=\frac{1}{m}\overrightarrow{CP}$,$\overrightarrow{CB}=\frac{1}{n}\overrightarrow{CQ}$,
∴$\overrightarrow{CG}=\frac{1}{3m}\overrightarrow{CP}$+$\frac{1}{3n}\overrightarrow{CQ}$.
∵P,G,Q三点共线,
∴$\frac{1}{3m}+\frac{1}{3n}=1$,
∴$\frac{1}{m}+\frac{1}{n}=3$
故答案为:3.
点评 本题考查了平面向量的线性运算的几何意义,平面向量的基本定理,属于中档题.


科目:高中数学 来源: 题型:解答题
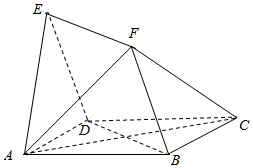 如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,AB=2,且FA=FC.
如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,AB=2,且FA=FC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}$ | B. | $\frac{{\sqrt{3}}}{2}-2$ | C. | $-\frac{{\sqrt{3}}}{2}-2$ | D. | $-\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
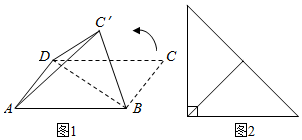
| A. | 等边三角形 | B. | 直角三角形 | ||
| C. | 两腰长都为$\frac{{\sqrt{3}}}{2}$的等腰三角形 | D. | 两腰长都为$\frac{{\sqrt{2}}}{2}$的等腰三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知三棱锥的三视图如图所示,其中侧视图是边长为$\sqrt{3}$的正三角形,则该几何体的外接球的体积为( )
已知三棱锥的三视图如图所示,其中侧视图是边长为$\sqrt{3}$的正三角形,则该几何体的外接球的体积为( )| A. | $\frac{16π}{3}$ | B. | $\frac{32}{3}π$ | C. | 4$\sqrt{3}$π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
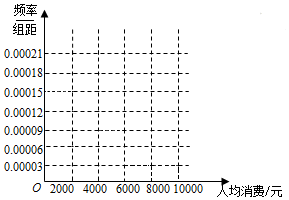 某旅游为了解2015年国庆节期间参加某境外旅游线路的游客的人均购物消费情况,随机对50人做了问卷调查,得如下频数分布表:
某旅游为了解2015年国庆节期间参加某境外旅游线路的游客的人均购物消费情况,随机对50人做了问卷调查,得如下频数分布表:| 人均购物消费情况 | [0,2000] | (2000,4000] | (4000,6000] | (6000,8000] | (8000,10000] |
| 额数 | 15 | 20 | 9 | 3 | 3 |
| 人均购物消费不超过4000元 | 人均购物消费超过4000元 | 合计 | |
| 资助超过500元 | 30 | ||
| 资助不超过500元 | 6 | ||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
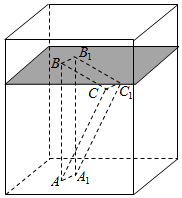 已知三棱柱ABC-A1B1C1,侧棱BB1⊥平面ABC,AB=2,AC=$\sqrt{3}$,AA1=$\frac{1}{4}$,AC⊥BC,将其放入一个水平放置的水槽中,使AA1在水槽底面内,平面ABB1A1与水槽底面垂直,且水面恰好经过棱BB1,现水槽底面出现一个洞,水位下降,则在水位下降过程中,几何体露出水面部分的面积S关于水位下降的高度h的图象大致为( )
已知三棱柱ABC-A1B1C1,侧棱BB1⊥平面ABC,AB=2,AC=$\sqrt{3}$,AA1=$\frac{1}{4}$,AC⊥BC,将其放入一个水平放置的水槽中,使AA1在水槽底面内,平面ABB1A1与水槽底面垂直,且水面恰好经过棱BB1,现水槽底面出现一个洞,水位下降,则在水位下降过程中,几何体露出水面部分的面积S关于水位下降的高度h的图象大致为( )| A. | 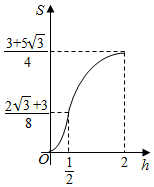 | B. | 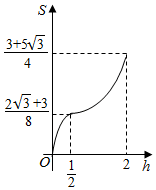 | ||
| C. | 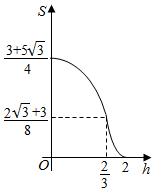 | D. | 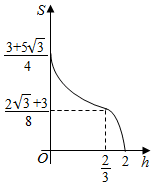 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com