
 已知三棱锥的三视图如图所示,其中侧视图是边长为$\sqrt{3}$的正三角形,则该几何体的外接球的体积为( )
已知三棱锥的三视图如图所示,其中侧视图是边长为$\sqrt{3}$的正三角形,则该几何体的外接球的体积为( )| A. | $\frac{16π}{3}$ | B. | $\frac{32}{3}π$ | C. | 4$\sqrt{3}$π | D. | 16π |
分析 由已知中的三视图,可得正视图底边对应棱的中点,到三棱锥各个顶点的距离相等,进而求出球半径,可得体积.
解答  解:由已知中的三视图,可得该几何体的直观图如图所示:
解:由已知中的三视图,可得该几何体的直观图如图所示:
取AB的中点F,AF的中点E,
由三视图可得:AB垂直平面CDE,且平面CDE为$\sqrt{3}$的正三角形,AB=1+3=4,
∴AF=BF=2,EF=1,
∴CF=DF=$\sqrt{{1}^{2}+{\sqrt{3}}^{2}}$=2,
故F即为棱锥外接球的球心,半径R=2,
故外接球的体积V=$\frac{4}{3}{πR}^{3}$=$\frac{32}{3}π$,
故选:B
点评 本题考查的知识点是由三视图,求体积和表面积,根据已知的三视图,判断几何体的形状是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | 2或$\sqrt{3}$ | B. | 2或$\frac{2\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
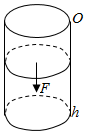 如图,在某一温度下,直径为0.2m,高为0.8m上端为活塞的圆柱体内某气体的压强p(N/m2)与体积V(m3)的函数关系式为p=$\frac{80}{V}$,而正压力F(N)与压强p(N/m2)的函数关系为F=pS,其中S(m2)为受力面积.设温度保持不变,要使气体的体积缩小为原来的一半.求活塞克服气体压力做多少功?
如图,在某一温度下,直径为0.2m,高为0.8m上端为活塞的圆柱体内某气体的压强p(N/m2)与体积V(m3)的函数关系式为p=$\frac{80}{V}$,而正压力F(N)与压强p(N/m2)的函数关系为F=pS,其中S(m2)为受力面积.设温度保持不变,要使气体的体积缩小为原来的一半.求活塞克服气体压力做多少功?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
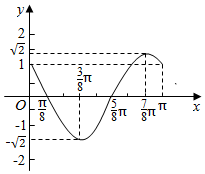
| A. | f(x)=2cos(2x+$\frac{π}{4}$) | B. | f(x)=-$\sqrt{2}$cos(x-$\frac{π}{4}$) | C. | f(x)=-$\sqrt{2}$cos(2x-$\frac{3π}{4}$) | D. | f(x)=$\sqrt{2}$cos(2x-$\frac{π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com