Question

11．在△ABC中，AB=2，BC=$\sqrt{10}$，AC=3．
（1）求$\overrightarrow{AB}•\overrightarrow{AC}$的值；
（2）若O是△ABC外心，求$\overrightarrow{AO}•\overrightarrow{BC}$的值
（3）若O为△ABC外心，$\overrightarrow{AO}=p\overrightarrow{AB}+q\overrightarrow{AC}$，求p，q的值．

Answer 1

分析 （1）利用余弦定理求出cosA，代入向量的数量积公式计算；
（2）过O作AB，AC的垂线，用$\overrightarrow{AB}，\overrightarrow{AC}$表示出$\overrightarrow{BC}$，利用向量数量积的定义式计算；
（3）将$\overrightarrow{AO}=p\overrightarrow{AB}+q\overrightarrow{AC}$两边分别乘$\overrightarrow{AB}，\overrightarrow{AC}$，列出方程组解出p，q．

解答 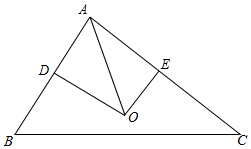解：（1）由余弦定理得cosA=$\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2AB•AC}$=$\frac{1}{4}$．
∴$\overrightarrow{AB}•\overrightarrow{AC}$=AB×AC×cosA=2×$3×\frac{1}{4}$=$\frac{3}{2}$．
（2）过O作OD⊥AB，OE⊥AC，则D，E分别是AB，AC的中点．
∴AD=$\frac{1}{2}AB=1$，AE=$\frac{1}{2}AC=\frac{3}{2}$．
∴$\overrightarrow{AO}•\overrightarrow{BC}$=$\overrightarrow{AO}•（\overrightarrow{BA}+\overrightarrow{AC}）$=$\overrightarrow{AO}•\overrightarrow{BA}$+$\overrightarrow{AO}•\overrightarrow{AC}$=-AB•AD+AC•AE=-2×1+3×$\frac{3}{2}$=$\frac{5}{2}$．
（3）∵$\overrightarrow{AO}=p\overrightarrow{AB}+q\overrightarrow{AC}$，∴$\left\{\begin{array}{l}{\overrightarrow{AO}•\overrightarrow{AB}=p{\overrightarrow{AB}}^{2}+q\overrightarrow{AB}•\overrightarrow{AC}}\\{\overrightarrow{AO}•\overrightarrow{AC}=p\overrightarrow{AB}•\overrightarrow{AC}+q{\overrightarrow{AC}}^{2}}\end{array}\right.$，
∵$\overrightarrow{AO}•\overrightarrow{AB}$=AB•AO•cos∠BAO=AB•AD=2，
$\overrightarrow{AO}•\overrightarrow{AC}$=AO•AC•cos∠CAO=AC•AE=$\frac{9}{2}$．
∴$\left\{\begin{array}{l}{2=4p+\frac{3}{2}q}\\{\frac{9}{2}=\frac{3}{2}p+9q}\end{array}\right.$，解得p=$\frac{1}{3}$，q=$\frac{4}{9}$．

点评 考查三角形外心的定义，余弦定理，以及数量积的运算及其计算公式，属于中档题．