
���� ������ƽ����������������������Ǻ�����ȱ任��Ӧ�ÿɵú�������ʽΪf��x��=$2sin��2��x+\frac{��}{6}��$������֪�������ڹ�ʽ������ص�ֵ��
������f��A��=1����$sin��2A+\frac{��}{6}��=\frac{1}{2}$����Ϸ�Χ$\frac{��}{6}��2A+\frac{��}{6}��\frac{13}{6}��$�����ɽ��A��ֵ�������Ҷ����ɵ�b2+c2-bc=3����b+c=3��������ã�b��c��ֵ�����������������ʽ���ɼ���ý⣮
��� ����������Ϊ12�֣�
�⣺����f��x��=a•b=${cos^2}��x-{sin^2}��x+2\sqrt{3}cos��x•sin��x$=$cos2��x+\sqrt{3}sin2��x$=$2sin��2��x+\frac{��}{6}��$������4�֣�
�ߦأ�0��
��$����f��x��������T=\frac{2��}{2��}=\frac{��}{��}=��$��
���=1����5�֣�
����$f��x��=2sin��2x+\frac{��}{6}��$��
�֡�f��A��=1��
��$sin��2A+\frac{��}{6}��=\frac{1}{2}$����$\frac{��}{6}��2A+\frac{��}{6}��\frac{13}{6}��$��
��$2A+\frac{��}{6}=\frac{5}{6}��$��
��$A=\frac{��}{3}$������8�֣�
�����Ҷ���֪$cosA=\frac{{{b^2}+{c^2}-{a^2}}}{2bc}$��
��b2+c2-bc=3����b+c=3��������ã�$\left\{\begin{array}{l}b=2\\ c=1\end{array}\right.��\left\{\begin{array}{l}b=1\\ c=2\end{array}\right.$������10�֣�
��${S_{��ABC}}=\frac{1}{2}bcsinA=\frac{{\sqrt{3}}}{2}$������12�֣�
���� ������Ҫ������ƽ����������������������Ǻ�����ȱ任��Ӧ�ã����ڹ�ʽ�����Ҷ����������������ʽ�Լ����Һ�����ͼ��������ڽ��������е��ۺ�Ӧ�ã�������ת��˼������ν��˼�룬�����е��⣮


 ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
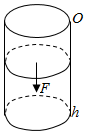 ��ͼ����ijһ�¶��£�ֱ��Ϊ0.2m����Ϊ0.8m�϶�Ϊ������Բ������ij�����ѹǿp��N/m2�������V��m3���ĺ�����ϵʽΪp=$\frac{80}{V}$������ѹ��F��N����ѹǿp��N/m2���ĺ�����ϵΪF=pS������S��m2��Ϊ������������¶ȱ��ֲ��䣬Ҫʹ����������СΪԭ����һ�룮������˷�����ѹ�������ٹ���
��ͼ����ijһ�¶��£�ֱ��Ϊ0.2m����Ϊ0.8m�϶�Ϊ������Բ������ij�����ѹǿp��N/m2�������V��m3���ĺ�����ϵʽΪp=$\frac{80}{V}$������ѹ��F��N����ѹǿp��N/m2���ĺ�����ϵΪF=pS������S��m2��Ϊ������������¶ȱ��ֲ��䣬Ҫʹ����������СΪԭ����һ�룮������˷�����ѹ�������ٹ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��$\frac{2}{7}$�� | B�� | ��$\frac{2}{7}$��$\frac{2}{3}$�� | C�� | ��$\frac{2}{3}$��$\frac{4}{5}$�� | D�� | ��$\frac{2}{7}$��$\frac{4}{5}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
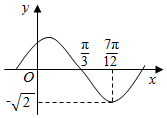 ����f��x��=Asin����x+�գ���A��0���أ�0���IJ���ͼ����ͼ��ʾ����$f��\frac{11��}{24}��$��ֵΪ��������
����f��x��=Asin����x+�գ���A��0���أ�0���IJ���ͼ����ͼ��ʾ����$f��\frac{11��}{24}��$��ֵΪ��������| A�� | $-\frac{{\sqrt{6}}}{2}$ | B�� | $-\frac{{\sqrt{3}}}{2}$ | C�� | $-\frac{{\sqrt{2}}}{2}$ | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com